6. Графы
6.1. Основные концепции и представление в памяти
Граф – это набор узлов (вершин) и связей между ними (рёбер). Каждая связь соединяет ровно два узла. Узлы, соединённые ребром, называются смежными или соседними. Рёбра, связанные с одним узлом, называют инцидентными ему. Под степенью вершины понимается количество инцидентных ей рёбер. Путь в графе – это последовательность вершин, в которой каждая следующая смежна с предыдущей. Циклом называют путь, в котором первая и последняя вершины совпадают.
Граф называют планарным, если его можно нарисовать на плоскости так, чтобы рёбра не пересекались. Граф может быть ориентированным (рёбра имеют направление) или неориентированным. Граф может быть взвешенным (каждое ребро имеет вес) или невзвешенным. Граф, в котором каждая пара вершин смежна, называют полным. Неориентированный полный граф с вершинами содержит рёбер. В зависимости от близости графа к полноте условно различают насыщенные и разреженные графы. У насыщенного графа число рёбер имеет порядок , у разреженного – .
Графы – незаменимые структуры данных, без которых не обходится ни одна сколько-либо сложная задача. Они являются универсальным способом моделирования связей между объектами. К тому же, деревья и списки можно рассматривать как частные случаи графов. Графы можно встретить в самых разных областях: в теории игр, социальных сетях, оптимизации транспортных потоков, маршрутизации в компьютерных сетях, даже нейронные сети – это тоже графы.
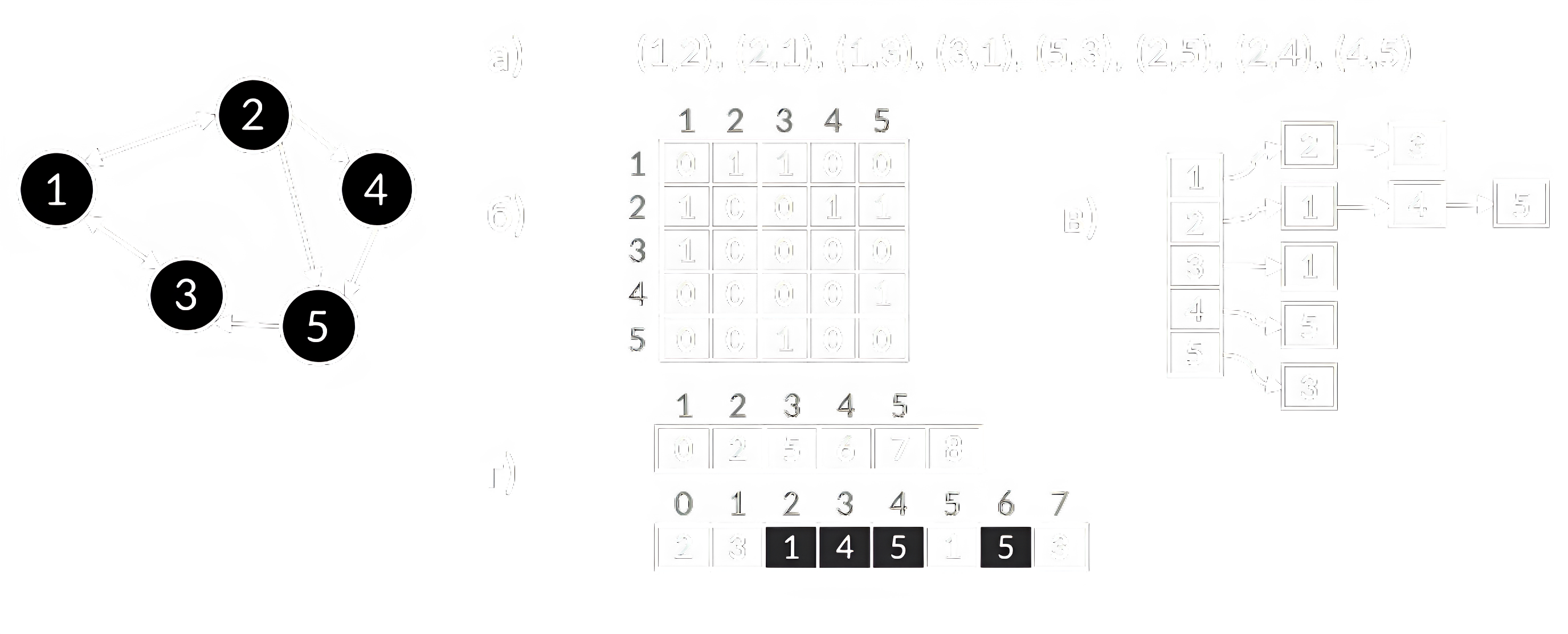
Возможны различные способы представления графа в памяти. Наиболее распространённые: список рёбер, списки смежности, матрица смежности (рисунок 16). Реже используется матрица инцидентности. Пусть – число вершин, – число рёбер, а – средняя степень вершины, тогда сложности, присущие различным представлениям, приведены в таблице 3.
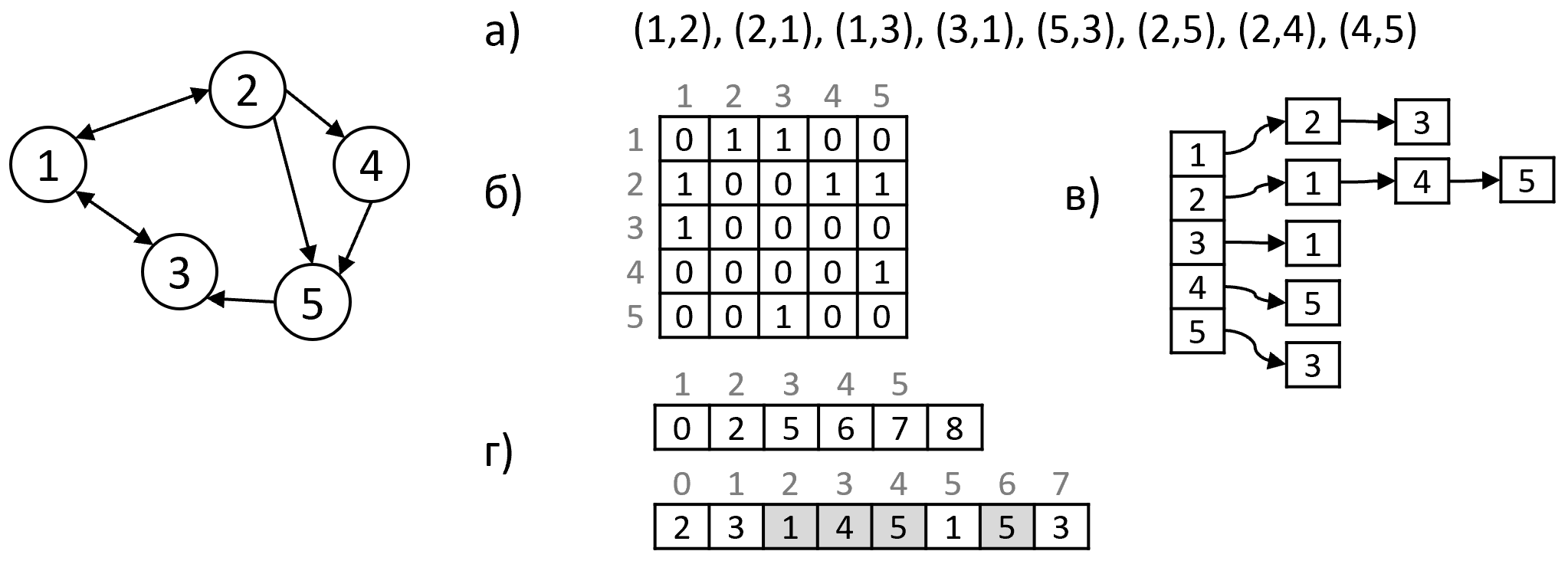
Таблица 3. Сложность операций на графе
| Представление | Память | Добавление узла | Добавление ребра | Проверка смежности | Обход смежных вершин |
|---|---|---|---|---|---|
| Список рёбер | |||||
| Списки смежности | |||||
| Матрица смежности |
Список рёбер – наиболее простой вариант, однако хорошо подходящий для алгоритмов на рёбрах, когда не часто необходимо искать соседей.
Списки смежности – это массив, в котором для каждой вершины хранится список её соседей. Для взвешенного графа в списке хранится ещё и вес ребра. Списки смежности эффективны для хранения разреженных графов. При неориентированном графе каждому ребру соответствуют записи в двух списках смежности. Для хранения списка смежных вершин можно использовать другие структуры: хеш-таблицы, сбалансированные деревья и т.д. При статичности данных для компактности и эффективного задействования процессорного кеша подойдёт один массив. Тогда ячейки оригинального массива содержат индексы начала и конца списка для соответствующей вершины.
Матрица смежности – это квадратная матрица, в которой элемент равен 1, если есть ребро из вершины в вершину , и 0 в противном случае. Для взвешенного графа в матрице хранится вес ребра. Матрица смежности эффективна для хранения насыщенных графов. При неориентированном графе матрица симметрична относительно главной диагонали.
6.2. Обход графа
Всякий алгоритм обхода графа заключается в том, чтобы, начиная с некоторой вершины, посетить все прочие не более одного раза, для чего необходимо как-то помечать посещённые узлы. Порядок посещения узлов определяется структурой данных, куда помещаются кандидаты на посещение. В общем случае без конкретики реализации алгоритм обхода абстрактно можно описать следующим образом:
def traverse(graph, start):
visited = init_set() # посещённые вершины
candidates = init_candidates() # кандидаты на посещение
candidates.push(start)
while candidates не пуста:
node = candidates.pop()
if node in visited:
continue
# Обработать узел
visited.add(node)
for each neighbor, смежный с node и ∉ visited:
candidates.push(neighbor)
visited может представлять массив булевых флагов или любую реализацию множества. candidates может быть стеком, очередью, очередью с приоритетом. Иногда visited называют закрытым списком (closed list, closed set), а candidates – открытым списком (open list, open set).
В процессе обхода, как правило, выстраивается так называемое дерево обхода, в котором для каждой вершины хранится ссылка на предка, по которому мы в неё попали. Это позволяет восстановить путь от начальной вершины до любой другой и хранить дополнительную информацию, связанную с обходом.
Поиск в графе – это обход, который останавливается при нахождении вершины, удовлетворяющей условию. Потому базовые алгоритмы можно называть как алгоритмами обхода, так и алгоритмами поиска. Основных таких алгоритмов два: поиск в ширину и поиск в глубину.
Поиск в глубину (Depth-First Search, DFS) – это обход, при котором кандидаты на посещение хранятся в стеке. При этом алгоритм двигается вглубь, откатываясь только при заходе в «тупик». Поиск в глубину может также быть реализован рекурсивно, тогда будет использоваться системный стек.
Для многих задач, решаемых поиском в глубину, необходимо при построении дерева обхода отмечать номера шагов, на которых алгоритм впервые заходит в вершину и возвращается из неё (метки времени). Например, для рекурсивной реализации это будет выглядеть так:
timer = 0
time_in = {}
time_out = {}
def dfs(u):
time_in[u] = timer++
for each v, смежный с u:
if v не посещён:
dfs(v)
time_out[u] = timer++
Эти метки будут обладать следующими свойствами:
- если – предок в дереве обхода, то ;
- два полуинтервала и либо не пересекаются, либо один вложен в другой;
- размер поддерева вершины (включая ) равен ;
Пример практической задачи, где используются эти свойства – упрощение запросов из БД товаров, категоризируемых иерархически. Пусть для дерева категорий предварительно расставлены метки времени при обходе в глубину и необходимо получить товары из всех подкатегорий категории с метками . Тогда достаточно вернуть товары, чья категория имеет метки, лежащие в полуинтервале .
Поиск в глубину применяется для нахождения циклов в графе, топологической сортировки, поиска путей и многого другого.
Поиск в ширину (Breadth-First Search, BFS) – это вариант обхода, при котором кандидаты на посещение хранятся в очереди. При этом сначала посещаются все вершины, смежные с начальной, затем все вершины, смежные с ними и т.д. Таким образом, дерево обхода выстраивается по уровням, а в полученном дереве путь от корня до любой другой вершины будет кратчайшим по числу рёбер. Поэтому при невзвешенном графе этот алгоритм подходит для поиска кратчайшего пути между двумя вершинами. Возможно адаптировать его и для взвешенного графа с небольшими целочисленными весами.
Кроме того, обход в ширину используется для поиска компонент связности, циклов, проверки двудольности и т.д.
6.3. Кратчайший путь в графе
Вариантов задачи поиска кратчайшего пути в графе существует несколько: между парой вершин, из заданной во все остальные, между каждыми парами вершин и т.д. При этом различают взвешенную задачу, где ищется кратчайший путь по сумме весов рёбер, и невзвешенную, когда ищется кратчайший по их числу. Невзвешенная задача – частный случай взвешенной, когда все рёбра имеют одинаковый вес. Подобные задачи возникают при оптимизации логистики, планировании проектов, реализации движения персонажей в играх, маршрутизации сетевых пакетов и т.д.
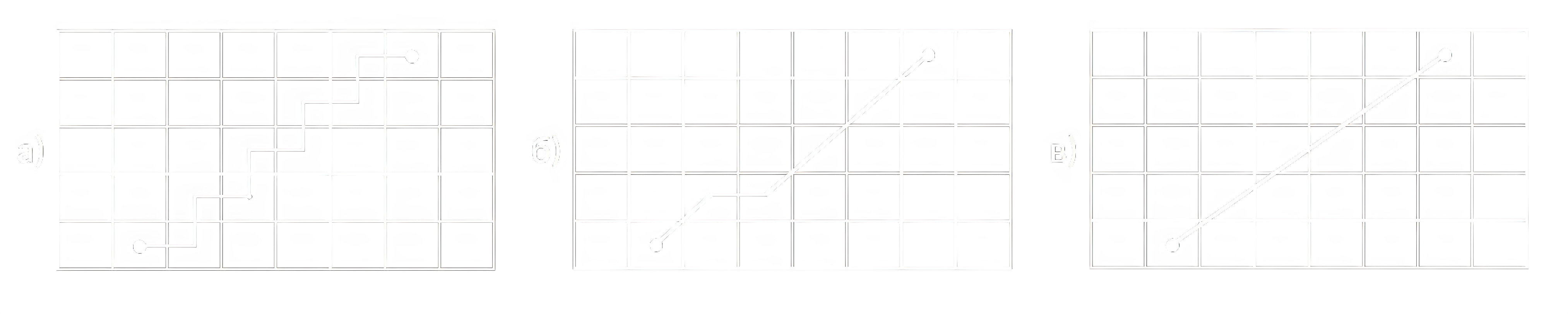
Ключевой вопрос для эффективности поиска путей в графе – это даже не сам алгоритм, а способ дискретизации пространства, в котором осуществляется маршрутизация. Представим уровень игры или карту местности с указанием расположения препятствий. Можно вручную разметить расположение развилок (узлов графа) и переходов между ними (рёбер). Можно использовать алгоритм, который сам построит подобный граф перемещений, учитывая желаемые нами свойства. А можно разбить всё пространство на «ячейки»/клетки» и построить граф на их основе. Тогда каждая ячейка будет узлом, а рёбра будут соединять смежные ячейки. В качестве формы ячеек могут выступать квадраты, шестиугольники, треугольники и другие. Если все ячейки одинаковы по размеру, это называют равномерной сеткой. Ещё один практикуемый подход – построение так называемых диаграмм Вороного, где каждая ячейка представляет собой область, ближайшую к определённой точке. На рисунке 17 приведены примеры некоторых вариантов дискретизации. Это очень сильно влияет на размеры графа (а значит, производительность) и свойства получаемых путей. У всех подходов свои преимущества и области применения. Кроме того, возможен иерархический подход, когда на разных уровнях детализации используются разные графы.

На этапе формирования графа учитываются особенности пространства вроде препятствий (отсутствие рёбер между ячейками), телепортов (добавление рёбер между удалёнными точками), а также устанавливаются веса перемещений по рёбрам. Семантика весов может быть разной: время прохождения, расстояние, стоимость и т.д. Благодаря им можно регулировать поведение персонажей, например, заставлять их предпочитать перемещение по дорогам, избегать слабо проходимые зоны и т.д.
Для поиска кратчайшего пути в невзвешенном графе, как уже было сказано, подойдёт обычный поиск в ширину. Применительно к сеткам использование принципов обхода в ширину реализует алгоритм Ли (волновой алгоритм). Он вводит концепцию волны, которая постепенно распространяется от начальной точки, захватывая все доступные ячейки. Каждая ячейка помечается номером шага, на котором она была достигнута (по сути это уровень в дереве обхода в ширину). Алгоритм завершается, когда волна достигнет целевой ячейки (если интересует только путь до неё) или когда волне больше некуда распространяться. Путь восстанавливается в обратном порядке от цели до источника путём поиска ячейки с наименьшим номером в соседних ячейках.
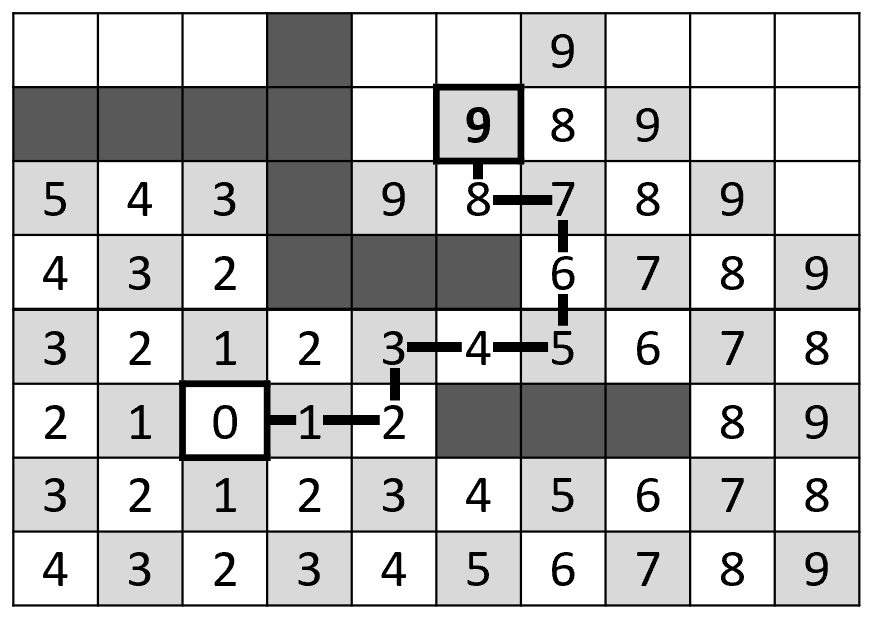
Волновой алгоритм или, в более общем случае, поиск в ширину, можно производить не из одной точки. Классический пример использования этого приёма – двунаправленный поиск. Если одновременно на каждой итерации делать шаг поиска от начальной точки и от конечной до момента их столкновения, то можно существенно ускорить алгоритм. При этом прямой поиск найдёт первую половину пути (от начальной до ячейки столкновения), а обратный – вторую (от ячейки столкновения, до конечной).
Алгоритм Дейкстры позволяет найти кратчайшие пути от заданной вершины до всех остальных в графе без рёбер отрицательного веса. Он использует очередь с приоритетом, чтобы на каждом шаге рассматривать вершину с наименьшим известным расстоянием до начальной. Алгоритм позволяет найти кратчайший путь от заданной вершины до всех остальных, а не только одной целевой.
def dijkstra(graph, start):
distances = { ∞ для каждого узла в graph }
distances[start] = 0
previous = { None для каждого узла в graph }
# Очередь вершин (min-heap), приоритеты – значения из distances
candidates = init_priority_queue(distances)
candidates.push(start)
while candidates не пуста:
vertice = candidates.pop()
for each neighbor, смежный с vertice:
new_distance = distances[vertice] + (вес ребра между vertice и neighbor)
if distances[neighbor] > new_distance:
# Найден более короткий путь до соседа, обновляем расстояние
distances[neighbor] = new_distance
previous[neighbor] = vertice
candidates.push(neighbor)
return distances, previous
После выполнения данного алгоритма длины кратчайших путей до всех вершин хранятся в distances, а сами пути можно восстановить по ссылкам в previous, где previous[vertice] – это предыдущая вершина на пути до vertice.
Временная сложность Дейкстры определяется реализацией очереди с приоритетом. Для насыщенных графов рациональнее искать линейно в массиве. Тогда получим асимптотику . Реализация же на бинарной куче эффективна для разрежённых графов, давая (что выродится в для насыщенного графа).
В алгоритме Дейкстра в качестве приоритета используется расстояние от начальной вершины. Это необходимо для корректной работы алгоритма, но не соответствует логике скорейшего поиска пути к цели. Поэтому может возникнуть идея использовать некую метрику того, насколько узел близок к целевому. Так первыми будут рассматриваться наиболее перспективные пути. Это подводит нас к алгоритмам эвристического поиска.
Эвристические алгоритмы используют в своей работе эвристики – некие приближённые оценки или интуитивные правила. В данной задаче эвристикой будет являться оценка расстояния от указанной вершины до цели. Как будет сказано в одной из глав следующей части, главный приём получения эвристических оценок – релаксация ограничений. В данном случае оценку можно получить из логики отбрасывания ограничений на проходимость. Т.е. предположить, что препятствий между двумя точками нет и просто оценить прямой путь между ними. Для квадратной сетки при учёте различных вариантов перемещения могут использоваться следующие метрики:
- манхэттенское расстояние (передвижение только вдоль осей) – ;
- диагональное расстояние (передвижение вдоль осей и по диагонали) – ;
- евклидово расстояние (без ограничений на передвижение) – .

Для взвешенного графа необходимо делать поправку на веса. Например, домножать на средний вес ребра.
Алгоритм, который мы получим, используя в качестве приоритетов для очереди кандидатов только подобную эвристическую оценку, и остановив поиск при нахождении целевой вершины, называется жадным алгоритмом по первому наилучшему соответствию (англ. Best First Search, BFS). Жадными называют такие алгоритмы, которые на каждом своём шаге принимают локально оптимальные решения: такие, которые кажутся наилучшими в данный момент, но не обязательно ведут к глобально оптимальному результату. В данном случае это олицетворяет принцип первичного обхода узлов, которые кажутся ведущими к цели. Этот алгоритм не гарантирует нахождение кратчайшего пути. Однако полученный путь с высокой долей вероятности будет довольно хорошим. Главное же преимущество алгоритма – скорость выполнения в большинстве ситуаций, поэтому он хорош там, где точность не столь важна.
Преимущества обоих подходов (Дейкстры и BFS) стремится объединить самый эффективный алгоритм на графах – алгоритм A*. Он использует в качестве приоритета для очереди кандидатов сумму расстояния от начальной вершины до текущей и эвристической оценки расстояния до цели. Таким образом, эта сумма сама является оценкой, но всего пути до цели, лежащего через текущую вершину.
Пусть узел дерева обхода описывается следующей структурой:
class SearchNode:
v: Vertice # вершина графа
g: float # длина пути от начала
h: float # оценка длины пути до цели
parent: Node # родительский узел в дереве обхода
Тогда процедуру алгоритма A* можно отразить псевдокодом:
def astar(graph, start, goal, heuristic):
start_node = SearchNode(v=start, g=0, h=heuristic(start, goal), parent=None)
candidates = init_priority_queue()
visited = init_set()
candidates.push(start_node, start_node.g + start_node.h)
while candidates не пуста:
search_node = candidates.pop()
vertice = search_node.v
if vertice in visited:
continue
if vertice == goal:
return search_node
visited.add(vertice)
for each neighbor, смежный с vertice и ∉ visited:
new_g = search_node.g + (вес ребра между vertice и neighbor)
new_h = heuristic(neighbor, goal)
new_node = SearchNode(v=neighbor, g=new_g, h=new_h, parent=search_node)
candidates.push(new_node, new_node.g + new_node.h)
return None
Полученный путь легко восстановить, проходя по ссылкам на родительские узлы.
В отличие от простого BFS, алгоритм A* гарантирует нахождение кратчайшего пути, но только при соблюдении двух условий относительно функции эвристической оценки :
- не должна переоценивать фактическое расстояние до цели;
- должно соблюдаться правило треугольника: если существуют пути и , то .
Оценки, получаемые релаксацией ограничений, являются нижними границами действительного расстояния на невзвешенной задаче. Однако в случае взвешенного графа гарантировать строгое соблюдение этого условия проблематично. Тогда A* будет давать, в общем случае, приближённый результат, но лучше BFS и быстрее Дейкстры. В целях оптимизации по времени это условие иногда даже нарушают намеренно, чтобы приблизить оценки к фактическим цифрам. Ведь чем ближе оценка к идеальному значению, тем меньше узлов переберёт алгоритм и быстрее завершится. Доказано, что число перебираемых узлов будет полиномиально, если
где - точная оценка.
A* очень гибок, имеет множество модификаций, повсеместно приме-няется в играх, робототехнике, телекоммуникациях, GPS-навигаторах и мно-гих других сферах.
6.4. Система непересекающихся множеств
Система непересекающихся множеств (англ. Disjoint-Set, DSU) – это структура данных, которая содержит набор непересекающихся непустых множеств, в каждом из которых зафиксирован один из элементов (представитель, representative). Она широко используется в ряде задач на графах, в том числе для построения остовных деревьев.
Система непересекающихся множеств поддерживает следующие операции:
MakeSet(x)– создать множество, содержащее только элементx;Union(x, y)– объединить множества, содержащие элементыxиy;Find(x)– найти представителя множества, которому принадлежит элементx.
Система непересекающихся множеств может быть реализована на различных структурах. Пусть – общее число элементов. Сложности операций для разных реализаций приведены в таблице 4. Можно хранить номера множеств для каждого элемента в статическом массиве. Но тогда объединение потребует прохода по всем элементам одного из множеств для их обновления. То же справедливо для представления подмножеств связными списками. В этом случае представители множеств располагаются в голове списков. Немного улучшить ситуацию с объединением может простая эвристика: при слиянии двух множеств всегда нужно меньшее прикреплять к большему.
Таблица 4. Сложность операций в системе непересекающихся множеств
| Реализация | MakeSet | Union | Find |
|---|---|---|---|
| Массив | |||
| Связный список | , если хранить указатель на голову в элементах | ||
| Дерево | ~ | ~ |
Наиболее оптимальный и сбалансированный вариант – реализация на лесе корневых деревьев. Тогда каждое множество хранится в виде дерева, а представитель располагается в его корне. При объединении двух множеств корень одного дерева подвешивается в качестве ребёнка к корню другого. Применяются две эвристики:
- Сжатие путей (англ. Path Compression) – при поиске представителя, т.е. подъёме в корень, у всех узлов на пути их родитель меняется на корень.
- Объединение по рангам (англ. Union by Rank) – при объединении двух деревьев меньшее подвешивается к большему. В качестве размера дерева рассматривается его ранг, т.е. по сути высота. У дерева из 1 узла ранг равен 0, при объединении деревьев с рангами и получается дерево с рангом .
Хоть сложность объединения и поиска представителя при такой реализации логарифмическая, на практике амортизационная оценка пропорциональна обратной функции Аккермана – безумно медленно растущей функции. Настолько, что её можно ограничить константой (5), не преодолимой для любых практических размеров. Т.е. эффективность операций фактически равна .
6.5. Остовное дерево
Граф называют связным, если между любой парой вершин существует путь. Иначе говорят, что он состоит из нескольких компонент связности – максимальных связных подграфов.
Остовное дерево (англ. Spanning Tree) – это подграф, который содержит все вершины исходного графа и является деревом. Задача нахождения остовного дерева заключается в отбрасывании лишних рёбер так, чтобы оставить минимально достаточное их количество для обеспечения связность, т.е. ребро для вершин. Очевидно, что у несвязного графа остовное дерево отсутствует (и мы далее будем предполагать, что на вход алгоритмам подаётся гарантированно связный граф). Для произвольного графа в общем случае остовное дерево не единственно.
На взвешенном графе формулируется задача о нахождении остовного дерева с минимальной суммой весов входящих в него рёбер (англ. Minimum Spanning Tree, MST). Некоторые свойства минимальных остовов:
- минимальный остов единственен, если веса всех рёбер различны;
- минимальный остов также является остовом, минимальным по произведению всех рёбер (если все веса положительны);
- минимальный остов является остовом с минимальным весом самого тяжёлого ребра;
- остов является минимальным тогда и только тогда, когда для любого ребра, не принадлежащего остову, цикл, образуемый этим ребром при добавлении к остову, не содержит рёбер тяжелее этого ребра.
Некоторые сферы, где могут возникать подобные задачи:
- оптимизация логистики (сеть дорог, трубопроводов, кабельных линий и т.д.);
- Spanning Tree Protocol в телекоммуникационных сетях стандарта Ethernet для предотвращения образования циклов в сети;
- построение или оптимизация сетей связи (компьютерных, телефонных, телекоммуникационных и т.д.), электроснабжения, водоснабжения и водоотведения;
- генерация лабиринтов в системах процедурной генерации уровней игр (т.к. остовное дерево по сути соответствует идеальному лабиринту).
Основные алгоритмы для построения минимального остовного дерева: алгоритм Краскала, Прима, Борувки. Их сложности зависят от представления графа, реализации очереди с приоритетом и системы непересекающихся множеств.
Псевдокод и основные шаги алгоритма Краскала приведены в листинге ... Главная идея заключается в постепенном добавлении рёбер в остовное дерево в порядке возрастания их весов, при этом проверяется, что добавление не приводит к циклу. Т.е. компонент связности постепенно должны объединиться в одну.
def kruskal(graph):
# Инициализируем минимальное остовное дерево
mst = init_mst()
# Создаём систему непересекающихся множеств и Помещаем
# все вершины в отдельные компоненты связности
dsu = init_dsu()
for each вершина v в графе:
dsu.make_set(v)
for each ребро edge в графе, отсортированное по возрастанию веса:
if dsu.find(edge.v) != dsu.find(edge.u):
# Ребро не образует цикл, добавляем его в остов
mst.add_edge(edge)
dsu.union(edge.v, edge.u)
# Если достигнута связность, останавливаемся
if dsu.count() == 1:
break
return mst
Инициализация компонент связности производится за , сортировка рёбер – , проход по рёбрам – . Операции с лесом корневых деревьев работают за . Тогда сложность алгоритма Краскала: . Если веса рёбер позволяют применять сортировку подсчётом или поразрядную, то можно получить .
Алгоритм Прима исходит из другой логики. Компонента связности остовного дерева постепенно наращивается, начиная со стартового узла, путём добавления новых вершин (и соединяющих с ними рёбер) так, чтобы не образовывался цикл. Варианты точно так же перебираются в порядке возрастания весов, а процедура останавливается, когда все вершины входят в остов.
def prim(graph, start):
# Инициализируем минимальное остовное дерево
mst = init_mst()
# Множество посещённых вершин
visited = init_set()
visited.add(start)
# Очередь рёбер по весу (min-heap)
edge_queue = init_priority_queue()
for each ребро edge, инцидентное start:
edge_queue.push(edge, edge.weight)
# Пока остов не содержит все вершины
while очередь edge_queue не пуста и visited не содержит все вершины:
edge = edge_queue.pop()
vertice = узел edge, не принадлежащий visited
if not vertice:
continue
# Добавляем вершину в остов
mst.add_edge(edge)
visited.add(vertice)
# Добавляем все рёбра из новой вершины в очередь
for each ребро next_edge, инцидентное vertice:
next_vertice = другая вершина ребра next_edge
if next_vertice not in visited:
edge_queue.push(next_edge, next_edge.weight)
return mst
Сложность данной реализации – . Если очередь с приоритетом реализовать на массиве, то получим сложность , что может быть оптимальнее для насыщенных графов.
Алгоритм Борувки схож с Краскалом, но на каждой итерации в остов добавляется не одно ребро, а по минимальному инцидентному ребру для каждой компоненты связности. Поэтому алгоритм хорошо распараллеливается. Более того, для планарных графов он работает за . Но он неэффективен на насыщенных графах, а реализация усложнена необходимостью в дополнительной фильтрации рёбер. На практике если Борувка и используется, то всё равно, когда число компонент связности станет небольшим, переключаются на Прима или Краскала.
6.6. Потоки в транспортной сети
Транспортной сетью называют ориентированный граф, в котором:
- выделены две вершины: исток (source) и сток (target, sink) ;
- из истока рёбра только выходят, в сток – только входят;
- любая другая вершина сети лежит на пути из в , при этом ;
- для каждого ребра задано число – его пропускная способность (ёмкость, capacity).
Поток через сеть – это функция , которая удовлетворяет условиям:
- поток через каждое ребро не превосходит его пропускную способность: ;
- поток из в противоположен потоку из в : ;
- для каждой вершины выполняется условие , где – сумма потоков, входящих в вершину, а – сумма потоков, выходящих из неё.
Величина потока – это . Поток называется максимальным, если он имеет наибольшую величину среди всех возможных потоков через данную сеть. Задача о поиске максимального потока может возникать в физике, экономике и многих других сферах. К примеру, в железнодорожной, автомобильной, водопроводной или другой сети известна предельная нагрузка отдельных звеньев, и требуется определить максимальное количество пассажиров, товаров, вещества и т.д., которые можно провести по этой сети, и каким образом.
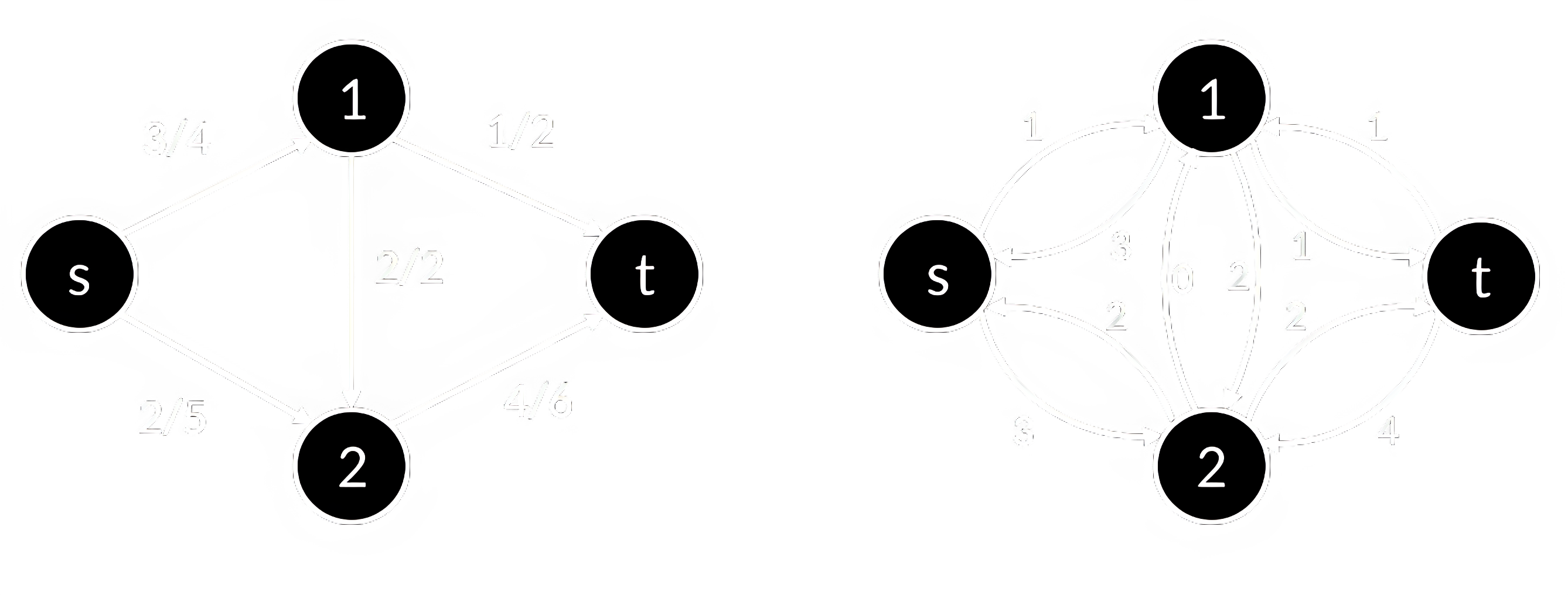
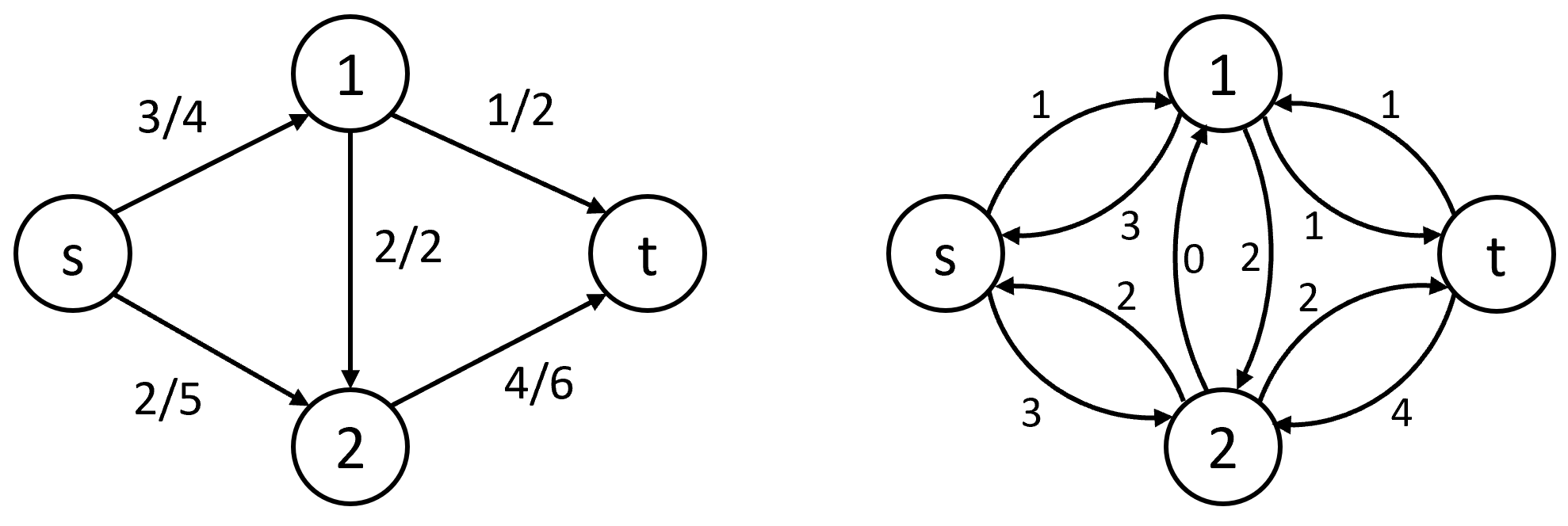
Найти максимальный поток можно при помощи алгоритма Форда-Фалкерсона. Он использует концепцию остаточной сети – графа, в котором для каждого ребра задано число – остаточная пропускная способность ребра (рисунок 20). Остаточная сеть показывает, сколько ещё можно пропустить по каждому ребру. Алгоритм Форда-Фалкерсона заключается в поиске в остаточной сети пути из истока в сток и увеличении потока через них. Процесс повторяется до тех пор, пока не останется пути из истока в сток.
def ford_fulkerson(graph, source, target):
flow = { 0 для каждого ребра в graph }
residual = { пропускная способность каждого ребра в graph }
while True:
# Находим путь в остаточной сети
path = find_path(graph, source, target, residual)
if not path:
break
# Увеличиваем поток через найденный путь
additional_flow = min(residual[(u, v)] для каждого ребра (u, v) в path)
for each ребро (u, v) в path:
flow[(u, v)] += additional_flow
residual[(u, v)] -= additional_flow
return flow
Сложность алгоритма Форда-Фалкерсона зависит от сложности поиска пути в остаточной сети. Если использовать поиск в глубину, то получим сложность , где – величина максимального потока. Алгоритм гарантированно сходится только для целых пропускных способностей. Если же заменить поиск в глубину на поиск в ширину (и искать кратчайший увеличивающий путь на каждом шаге), то получится алгоритм Эдмондса-Карпа, который сходится для любвых вещественных пропускных способностей и работает за .
Ещё один алгоритм поиска максимального потока – метод предпотока. Предпоток отличается ослабленным условием сохранения потока: для всех . Это означает, что поток может «заливаться» в вершину, но не обязательно должен «выливаться» из неё. Такая вершина с избыточным входящим потоком называется переполненной. Предпоток является потоком тогда и только тогда, когда переполненные вершины отсутствуют.
Метод проталкивания предпотока использует аналогию с ёмкостями воды (узлы), соединёнными шлангами (рёбрами). Вода может протекать из одной ёмкости в другую под действием гравитации. Поэтому с каждым узлом-ёмкостью ассоциирована высота . При этом начальная высота истока , стока – . Вода может перетечь из в , если , вершина переполнена и остаточная пропускная способность . Эта операция называется проталкиванием (push):
def push(u, v, flow, capacity, excess):
delta = min(excess[u], capacity[(u, v)] - flow[(u, v)])
flow[(u, v)] += delta
flow[(v, u)] -= delta
excess[u] -= delta
excess[v] += delta
Когда нигде больше проталкивание невозможно, необходимо поднять переполненную вершину выше, чтобы дать потоку распространиться дальше. Это операция подъёма (relabel):
def relabel(u, height, flow, capacity, graph):
edges = { (u, v): capacity[(u, v)] - flow[(u, v)] > 0 }
min_height = min(height[v] for (u, v) in edges)
height[u] = min_height + 1
Сам алгоритм заключается в последовательном применении операций push и relabel до тех пор, пока не останется переполненных вершин:
def push_relabel(graph, source, target):
height = { 0 для каждой вершины в graph }
excess = { 0 для каждой вершины в graph }
flow = { 0 для каждого ребра в graph }
capacity = { пропускная способность каждого ребра в graph }
# Инициализация
height[source] = количество вершин graph
for each ребро (source, v) в graph:
flow[(source, v)] = capacity[(source, v)]
flow[(v, source)] = -capacity[(source, v)]
excess[v] = capacity[(source, v)]
excess[source] -= capacity[(source, v)]
# Основной цикл
while существует вершина u != source, u != target с excess[u] > 0:
if существует сосед v с capacity[(u, v)] - flow[(u, v)] > 0 и height[u] == height[v] + 1:
push(u, v, flow, capacity, excess)
else:
relabel(u, height, flow, capacity, graph)
return flow
Подобная наивная версия имеет сложность , но возможны оптимизации, обеспечивающие , и даже ещё более эффективные. Потому алгоритм предпотока предпочтительнее Форда-Фалкерсона, чья практичная реализация (Эндмондса-Карпа) даёт .
В задаче о потоке минимальной стоимости (англ. Minimum Cost Flow, MCF) каждому ребру задаётся не только пропускная способность , но и стоимость за единицу потока. Задача заключается в нахождении потока максимальной величины, при котором его стоимость минимальна.
Задача решаема методом увеличивающих путей, т.е. модификацией всё того же алгоритма Форда-Фалкерсона. Отличие состоит в том, что при поиске пути в остаточной сети необходимо выбирать минимальный по стоимости. Этим же алгоритмом можно найти и поток минимальной стоимости заданной конкретной величины . Для этого если на очередной итерации увеличение величины потока позволяет достичь или превысить , то следует увеличить поток только на недостающее значение и завершить алгоритм.
Интересный случай применения алгоритмов поиска потока заключается в решении задачи о назначениях. Она формулируется следующим образом. Имеется заказов и станков. Про каждый заказ известна стоимость его изготовления на каждом станке – . На каждом станке можно выполнять только один заказ. Требуется распределить все заказы по станкам так, чтобы минимизировать суммарную стоимость.
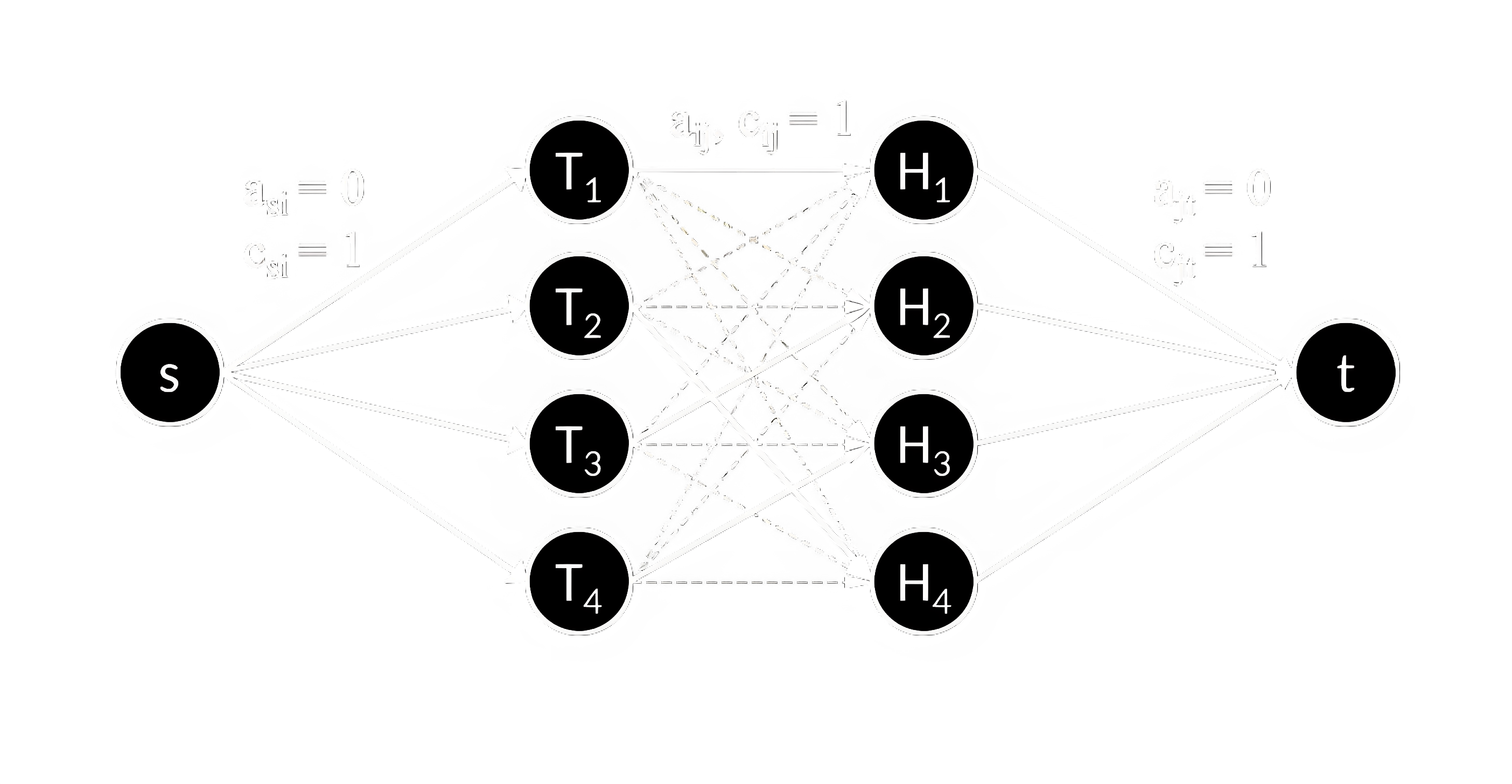
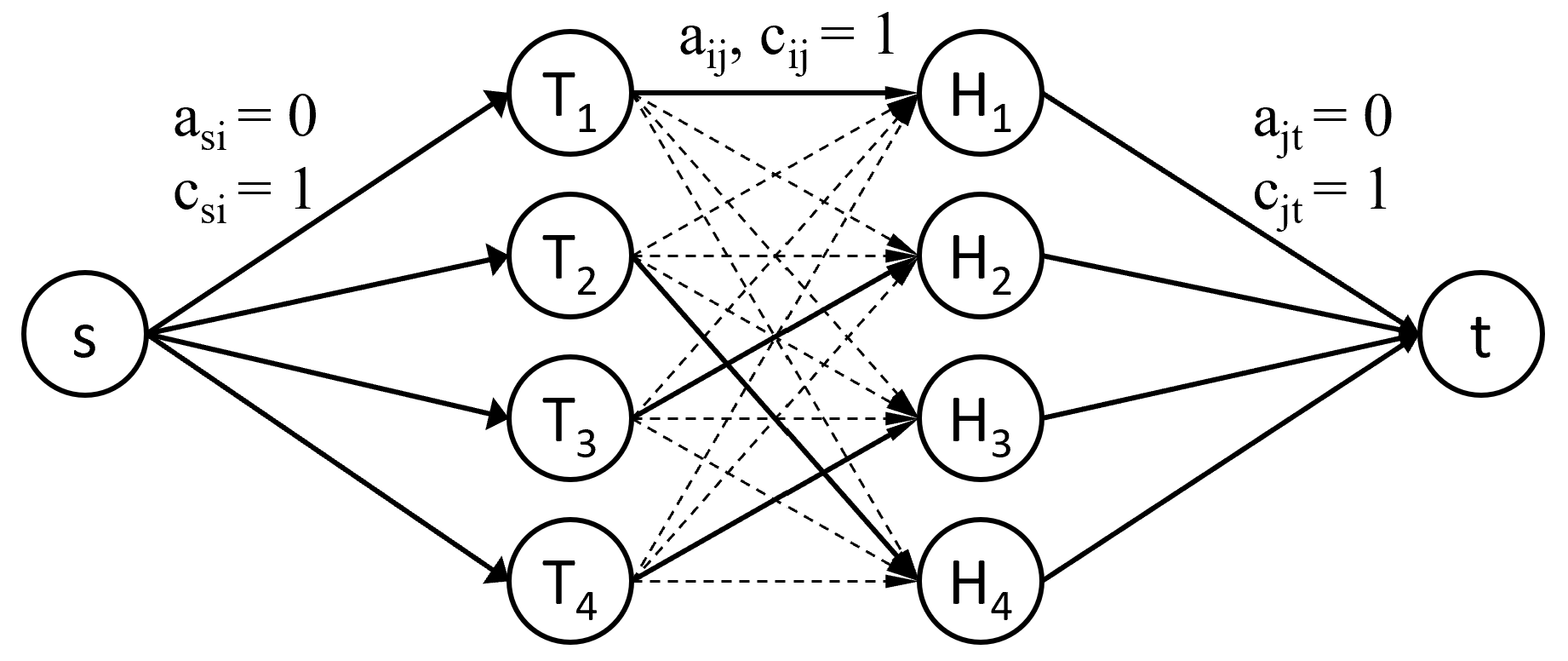
Для сведения этой задачи к задаче на поток необходимо построить двудольный граф транспортной сети (рисунок 21). Двудольным называется граф, вершины которого можно разбить на два множества так, что все рёбра соединяют вершины из разных множеств. Имеется исток , сток , в первой доле находятся вершин (заказы), во второй – тоже (станки). Между каждой вершиной первой доли и второй доли проведём ребро с пропускной способностью 1 и стоимостью . От истока проведём рёбра ко всем вершинам первой доли с пропускной способностью 1 и стоимостью 0. От каждой вершины второй доли к стоку проведём ребро с пропускной способностью 1 и стоимостью 0. После решения задачи о максимальном потоке минимальной стоимости получим искомое оптимальное распределение заказов по станкам, которое отражено рёбрами, через которые установился поток.
6.7. Прочие задачи на графах
Ещё один класс задач на графах связан с поиском разрезов – наборов рёбер, при удалении которых граф разбивается на компоненты связности. В транспортной сети выделяют s-t разрез – минимальный по величине разрез, который разрывает связь между истоком и стоком. Под пропускной способностью такого разреза понимается сумма пропускных способностей входящих в него рёбер.
Теорема Форда-Фалкерсона утверждает, что максимальный поток в транспортной сети равен пропускной способности минимального s-t разреза. Таким образом, задача о поиске минимального s-t разреза сводима к поиску максимального потока (и наоборот).
Для некоторых задач на разрезы не s-t типа также существуют эффективные узкоспециализированные алгоритмы. Например, Алгоритм Штёр-Вагнера для поиска минимального разреза в неориентированном графе. Но многие прочие относятся к классу NP-полных и требуют экспоненциального времени для подбора решения. Что это значит и как подступаться к решению подобных задач, будет рассматриваться во второй части пособия. Простой пример такой задачи – поиск максимального разреза (англ. Max Cut). Задачи о разрезах возникают при поиске слабых мест в сетях и коммуникациях, кластеризации, сегментации изображений и т.д.
Задача топологической сортировки ориентированного ациклического графа заключается в указании такого линейного порядка на его вершинах, чтобы любое ребро вело от вершины с меньшим порядковым номером к вершине с большим номером. Если в графе есть циклы, то такого порядка не существует. Примеры сфер, где на множестве объектов с заданными зависимостями необходимо выстроить не нарушающий их порядок:
- распараллеливание алгоритмов;
- сборка исходных текстов программ;
- построение планов выполнения задач;
- установка ПО или библиотек менеджерами зависимостей.
Топологическая сортировка может быть осуществлена при помощи поиска в глубину. Достаточно упорядочить вершины по , т.е. по времени выхода.
Другая задача, решаемая с помощью поиска в глубину – поиск точек сочленения. Вершина называется точкой сочленения, если её удаление разрывает связность графа. Пусть мы просматриваем рёбра из вершины . Если текущее ребро таково, что из вершины и из любого её потомка в дереве обхода в глубину нет обратного ребра в вершину или какого-либо её предка, то эта вершина является точкой сочленения.
Компонентой сильной связности называется максимальный по включению подграф ориентированного графа, в котором для любой пары вершин существует как путь от первой ко второй, так и от второй к первой. Поиск компонент сильной связности снова решаем лёгкой модификацией алгоритма поиска в глубину.
Среди циклов, возможно присутствующих в графах, выделяют:
- Эйлеров цикл – замкнутый путь, проходящий через каждое ребро графа ровно по одному разу;
- Гамильтонов путь – замкнутый путь, проходящий через каждую вершину графа ровно по одному разу.
Поиск подобных путей обычно требуется для оптимизации разного рода логистики. Первая задача имеет алгоритмы решения за полиномиальное время, однако вторая является NP-полной.
Ещё один класс задач на графах – задачи о раскраске вершин или рёбер. Раскраска вершин – это назначение каждой вершине цвета так, чтобы смежные вершины имели разные цвета. Минимальное число цветов, необходимое для раскраски графа, называется его хроматическим числом. Определение хроматического числа и самой раскраски является отдельной трудной задачей. Доказано, что для планарного графа хроматическое число равно 4. Соответствующая теорема называется теоремой о четырёх красках и примечательна тем, что стала первой крупной теоремой, доказанной с применением компьютера.
Число различных задач на графах поистине огромно, поэтому даже упомянуть их все не представляется сколько-либо возможным. Вот лишь некоторые из прочих:
- планарная укладка графа (изображение графа на плоскости так, чтобы рёбра не пересекались);
- задачи о покрытии вершин и рёбер;
- задачи о паросочетаниях в двудольном графе;
- поиск максимального клика (независимого подмножества вершин, в котором любые две вершины смежны);
- и многие другие.
В следующей части будут в том числе рассмотрены подходы к решению некоторых из упомянутых ранее трудных задач. Но главное, что сами эти подходы, а также многие прочие алгоритмы и концепции, о которых будет идти речь, будут основываться всё на той же теории графов. Поэтому трудно переоценить её фундаментальную значимость.