4. Очередь с приоритетом
4.1. Наивные реализации
Очередь с приоритетом (Priority Queue) отражает концепцию обработки элементов не в порядке поступления, как в обычной очереди, а в порядке приоритетности, отражённой в некой числовой метрике, приписанной элементам. Подобное требуется, например, в различных жадных и эвристических алгоритмах, о которых будет говориться далее в рамках курса.
Интерфейс очереди с приоритетом должен содержать операции:
Push(вставка элемента);Pop(изъятие самого приоритетного элемента);Increase(увеличение приоритета элемента);Merge(слияние с другой очередью).
В самом простом случае для реализации концепции очереди с приоритетом достаточно линейной структуры (массива или связного списка), хранящей пары ключ (приоритет) и соответствующее значение. Возможны два подхода: с ранними и ленивыми вычислениями. Идея ленивых вычислений в широком смысле заключается в их откладывании до тех пор, пока не понадобится результат. В данном случае из этого следует, что элементы в массиве или списке могут храниться в произвольном порядке, а операция получения очередного элемента потребует линейного поиска самого приоритетного на данный момент.
При ранних вычислениях всё подготавливается заранее, т.е. в данном случае предполагается поддерживать последовательность в отсортированном виде, чтобы было ясно, где лежит самый приоритетный элемент (в самом конце последовательности). Для этого при вставке элементу необходимо найти подходящее место, не нарушающее отсортированный порядок. Сложности основных операций, которые будут получены для различных вариантов реализации, приведены в таблице 2.
Таблица 2. Сложность наивных реализаций очереди с приоритетом
| Push | Pop | Increase | Merge | |
|---|---|---|---|---|
| Отсортированный массив | ||||
| Неотсортированный массив | ||||
| Отсортированный список | ||||
| Неотсортированный список |
4.2. Бинарная куча
Более эффективные реализации очереди с приоритетом основываются на древовидных структурах, называемых кучами (Heap). Различают невозрастающую и неубывающую кучу. В невозрастающей (Max Heap) куче ключ родительского узла всегда больше или равен ключей дочерних узлов, а в неубывающей (Min Heap) – меньше или равен. Таким образом, в корне кучи всегда находится элемент с максимальным (для Max Heap) или минимальным (для Min Heap) ключом. Если рассматривать в качестве ключей приоритеты, то это и будет самый приоритетный элемент. Далее для простоты условимся, что приоритетность определяется максимальным значением и используется невозрастающая куча.
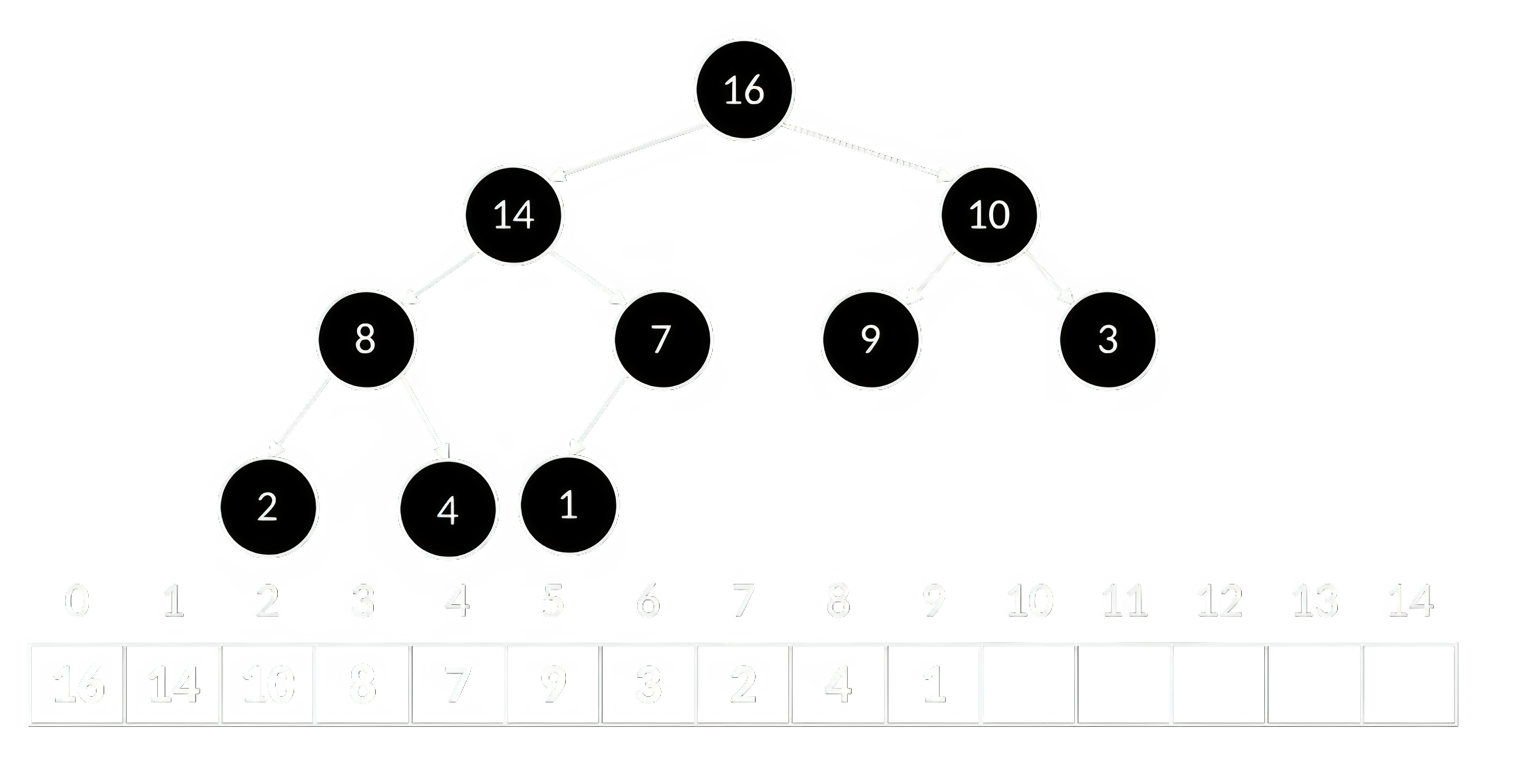
Существует множество подвидов кучи, но наиболее часто на практике применяется бинарная куча (Binary Heap, двоичная куча, пирамида). Она представляет собой бинарное (двоичное) дерево, т.е. каждый узел имеет не более двух детей (левый и правый). Бинарная куча обладающее свойством полноты: все уровни дерева заполнены, кроме, возможно, последнего. Причём последний уровень заполняется слева направо, не допуская пустых позиций. Благодаря этому, бинарная куча может быть представлена в виде массива, в котором элементы хранятся в порядке обхода по уровням слева направо (рисунок 6). Корень кучи будет находиться в ячейке с индексом 0, для узла с индексом его родитель будет иметь индекс , а дети – и .
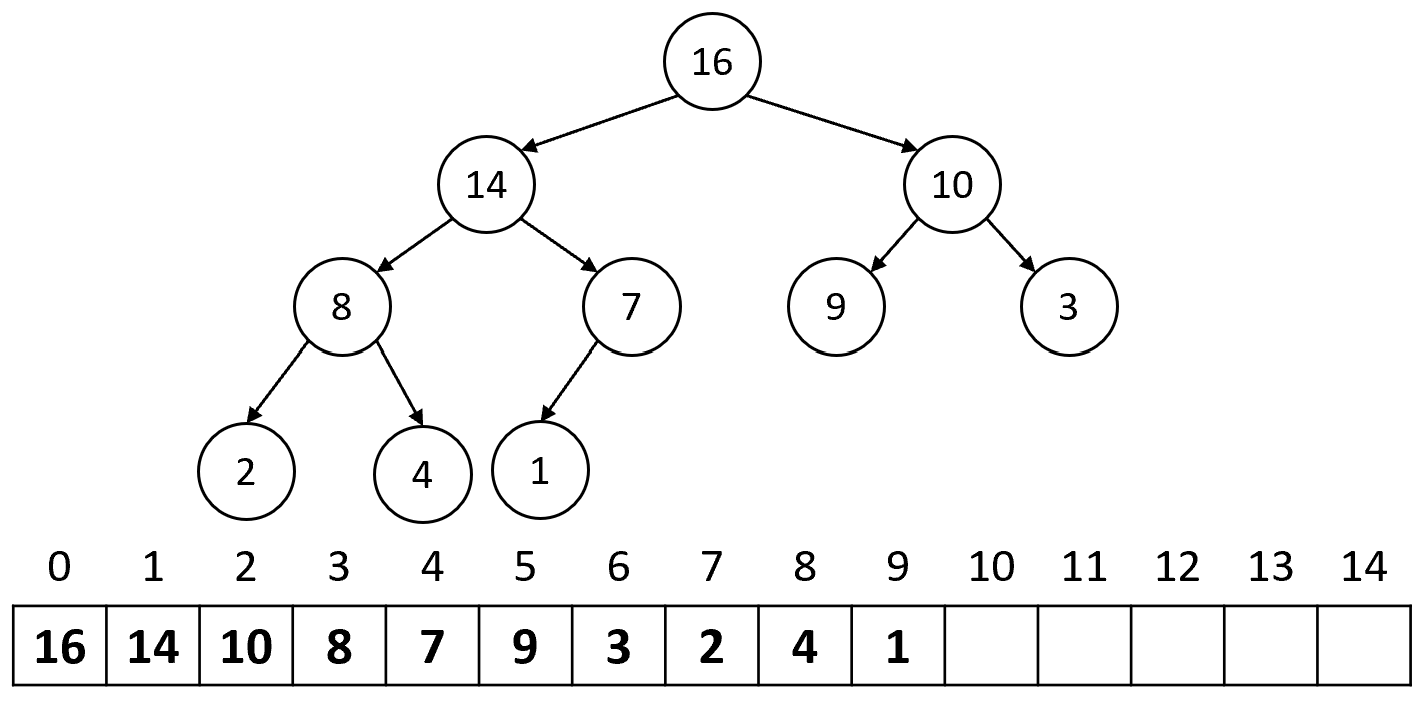
Основополагающими для реализации бинарной кучи являются операции восстановления свойств кучи: HeapifyUp (снизу вверх) и HeapifyDown (сверху вниз). Они выполняют восстановление свойств кучи после вставки и удаления элемента соответственно.
Начнём с операции вставки (Push). Для сохранения полноты дерева новая пара помещается в первую свободную позицию на последнем уровне, т.е. в конец массива. Это может нарушить свойство кучи, поэтому затем необходимо выполнить HeapifyUp начиная с индекса вставленного элемента. Эта процедура обменивает вставленный элемент с его родителем, если ключ родителя меньше ключа вставленного элемента. Обмены продолжаются до тех пор, пока элемент не встанет на место, не нарушающее свойство кучи или не будет достигнут корень (листинг 4).
def heapify_up(heap, index):
while index > 0 and heap[index] > heap[(index - 1) // 2]:
parent = (index - 1) // 2
heap[parent], heap[index] = heap[index], heap[parent]
index = parent
При извлечении максимального элемента из кучи (операция Pop) его место занимает последний элемент, и для восстановления свойств кучи необходимо выполнить HeapifyDown, начиная с корня (листинг 5). Элемент сравнивается с максимальным из детей, и если тот оказался больше, то происходит обмен. Обмены продолжаются до тех пор, пока элемент не встанет на место, не нарушающее свойство кучи, или не будет достигнут листовой уровень.
def heapify_down(heap, index):
n = len(heap)
while index < n:
left = 2 * index + 1
right = 2 * index + 2
largest = index
if (left < n and heap[left] > heap[largest]):
largest = left
if (right < n and heap[right] > heap[largest]):
largest = right
if (largest == index):
break
heap[index], heap[largest] = heap[largest], heap[index]
index = largest
Реализация операции Increase (увеличение приоритета элемента) сводится к поиску (за линейное время, если не использовать вспомогательные структуры), изменению приоритета и последующему HeapifyUp.
Немаловажной особенностью бинарной кучи является возможность её построения по месту (в произвольном массиве) за линейное время (листинг 6). Для этого необходимо последовательно вызывать HeapifyDown для всех узлов, имеющих хотя бы одного потомка. Благодаря этому слияние куч (Merge) также выполняется за линейное время: достаточно просто склеить массивы и построить кучу по месту.
def build_heap(heap):
n = len(heap) // 2 - 1
for i = n; i >= 0; i--:
heapify_down(heap, i)
В полном бинарном дереве, к которым относится и бинарная куча, высота . Операции HeapifyUp и HeapifyDown проходятся по уровням дерева, поэтому их сложность . Операции вставки и извлечения кроме вызова восстановления свойств кучи выполняют лишь примитивные операции на массиве, поэтому их сложность также .