5. Словарь

5.1. Общая информация

Словарь (Dictionary, Map, ассоциативный массив) – это структура данных, которая позволяет хранить пары ключ-значение и осуществлять поиск по ключу. Предполагается, что ключи уникальны, т.е. не может быть двух пар с одинаковыми ключами.

Интерфейс словаря обязательно должен содержать следующие операции:

Insert (вставка пары ключ-значение);
Delete (удаление пары по ключу);
Lookup (поиск значения по ключу).

Существует огромное число вариантов реализации данного АТД. Как и всегда, в простом случае можно использовать обычный массив или связный список и линейно искать нужную пару при необходимости. В случае отсортированного массива можно будет использовать бинарный поиск, улучшив асимптотику поиска до $O(\log n)$ , но расплатившись линейной сложностью вставки. Для сколько-либо эффективной же работы необходимо использовать более продвинутые структуры данных: бинарные деревья поиска, хеш-таблицы, префиксные деревья и другие.

Стоит также сразу оговориться, что множество (Set) – это частный случай словаря, когда значениями являются сами ключи. Поэтому для его реализации могут использоваться ровно те же структуры данных, что будут разбираться в данной главе. А если общее число элементов фиксировано и известно заранее, то для реализации множества можно использовать элементарную битовую маску (BitSet): значение 1 в ячейке $i$ означает, что элемент $i$ присутствует в множестве. Тогда все типовые операции над множествами сводятся к побитовым операциям на подобных масках.

5.2. Бинарное дерево поиска

Бинарное дерево поиска (Binary Search Tree, BST) – это бинарное дерево, в котором в каждом узле $x$ содержится отдельная пара ключ-значение, ключи всех узлов левого поддерева меньше, а правого поддерева – больше ключа $x$ .

Пусть узел BST описывается следующей структурой:

class BSTNode:
    key: int
    value: Any
    left: BSTNode
    right: BSTNode
    parent: BSTNode

Рассмотрим основные операции с подобной структурой. Поиск сводится к рекурсивному обходу дерева, сравнивая ключи и переходя в нужное поддерево:

def bst_search(root, key):
    if root is None or root.key == key:
        return root
    if key < root.key:
        return bst_search(root.left, key)
    return bst_search(root.right, key)

Для вставки также можно использовать рекурсивный подход, позволяющий сперва найти нужное место, а затем вставить новый узел:

def bst_insert(root, key, value):
    if root is None:
        return BSTNode(key, value)
    if key < root.key:
        root.left = bst_insert(root.left, key, value)
        root.left.parent = root
    else:
        root.right = bst_insert(root.right, key, value)
        root.right.parent = root
    return root

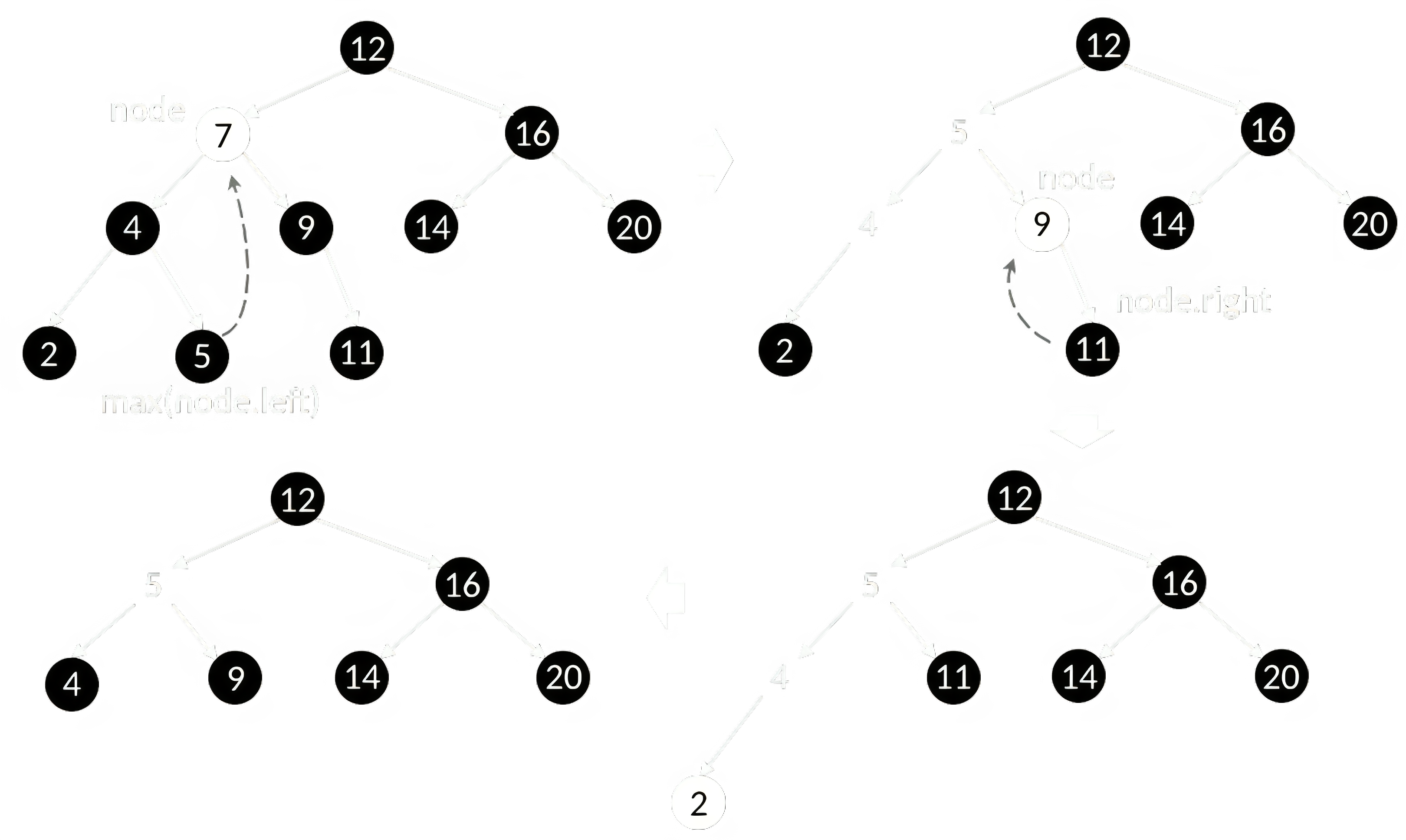
Удаление из BST не столь просто, т.к. в общем случае нельзя высвободить память под узел и обнулить все ссылки на него. Ведь у него могут быть дочерние узлы, а также нужно не нарушить свойства BST. Выделяют 3 случая (рисунок 7):

Удаляемый узел является листом дерева. В этом случае его можно просто удалить, не нарушив свойств BST.
Удаляемый узел имеет только одного потомка. В этом случае его можно удалить, а его потомка переместить на место удаляемого узла.
Удаляемый узел имеет двух потомков. В этом случае его место займёт узел с минимальным ключом из правого поддерева или максимальным ключом из левого поддерева.

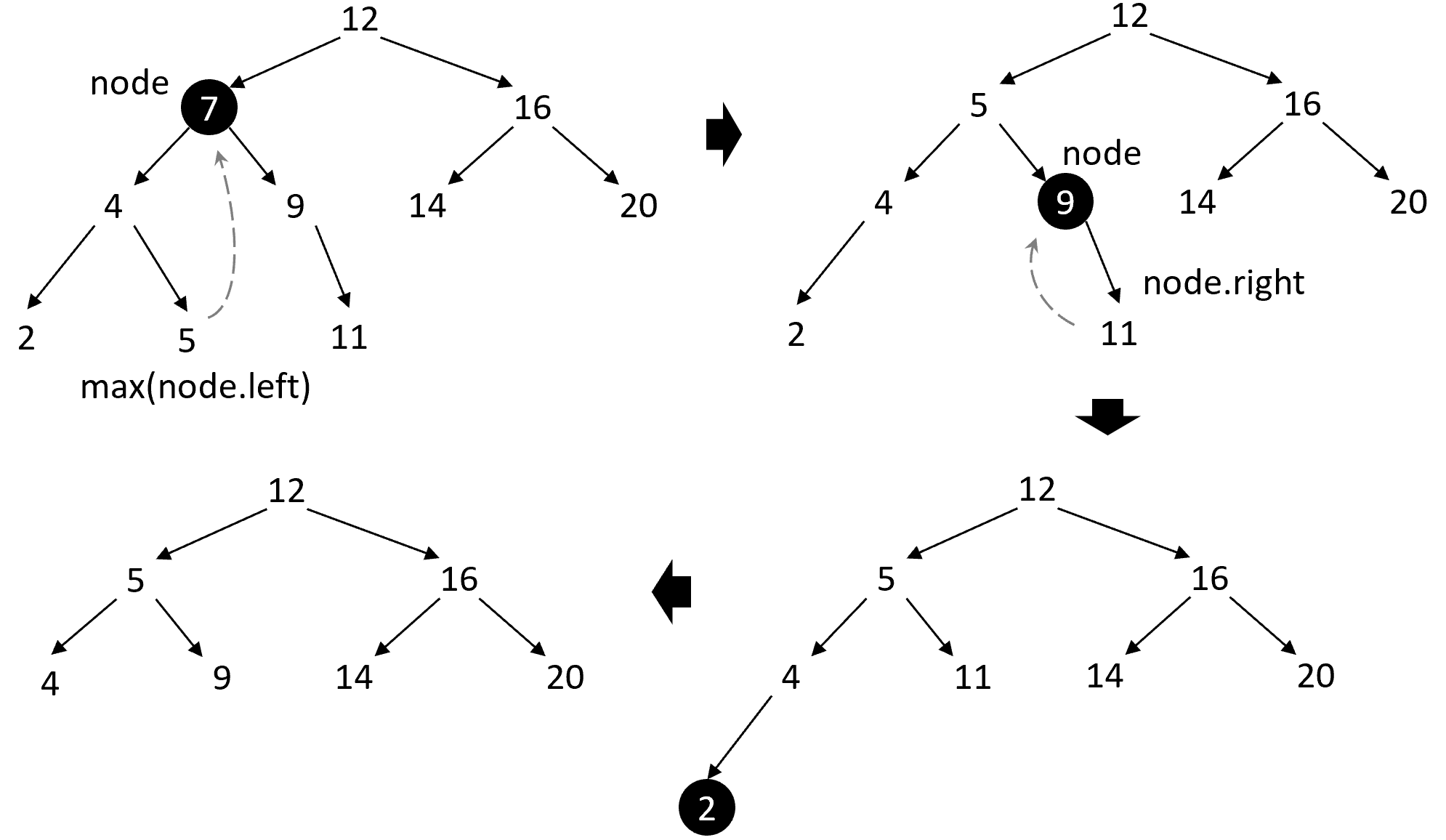
*Рисунок 7. Удаление из BST в разных случаях*

Элемент с максимальным ключом в BST или любом его поддереве находится в самом правом узле (необходимо двигаться только по правым дочерним ссылкам). Аналогично, элемент с минимальным ключом находится в самом левом узле. Таким образом, у узла, которым заменяется удаляемый в 3 случае узел, может быть максимум один потомок. Его изъятие, в свою очередь, сводится к случаям 1 или 2.

def bst_delete(root, key):
    if root is None:
        return None
    if key < root.key:
        root.left = bst_delete(root.left, key)
    elif key > root.key:
        root.right = bst_delete(root.right, key)
    else:
        if root.left is None:
            return root.right
        elif root.right is None:
            return root.left
        else:
            min_node = root.right
            while min_node.left is not None:
                min_node = min_node.left
            root.key = min_node.key
            root.right = bst_delete(root.right, min_node.key)
    return root

Логика замены в 3 случае исходит из того, что для гарантированного сохранения свойства BST необходимо подменить удаляемый ключ на предыдущий или последующий по порядку (среди всех ключей). Именно они в этом случае и являются максимальным и минимальным ключом в левом и правом поддереве соответственно. Для листового же узла последующий по значению ключа элемент ищется так: необходимо подняться по родительским ссылкам до тех пор, пока не будет достигнут узел, относительно которого текущий лежит в левом поддереве. Для поиска предыдущего – с точностью до наоборот.

Такая возможность эффективного обхода всех элементов в порядке возрастания или убывания ключа качественно отличает древовидные реализации словаря от хеш-таблиц. Потому в различных библиотеках их можно опознать по использованию в названии не только слова «Tree» (TreeMap и TreeSet в Java), но и слова «Sorted» (SortedDictionary и SortedSet в C#).

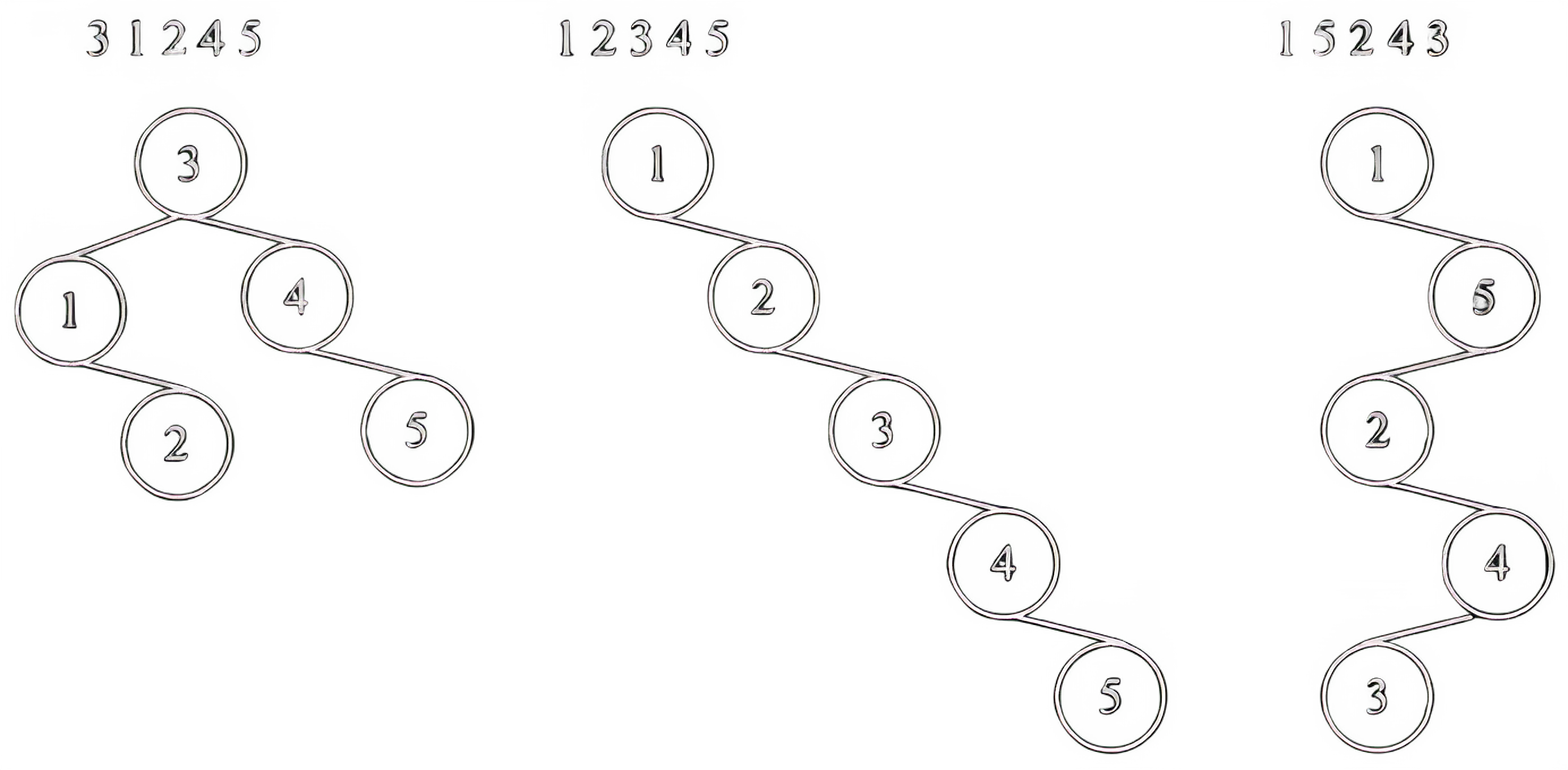
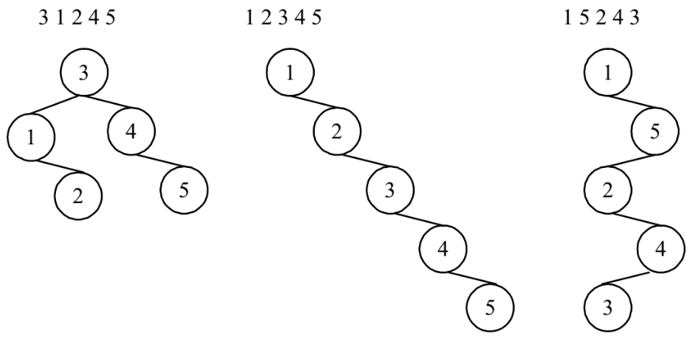
Асимптотика всех основных операций в BST (поиск, вставка, удаление, поиск максимального и минимального элемента) зависит от формы дерева. В худшем случае при неудачном порядке вставки элементов дерево вырождается в связный список (рисунок 8), и сложность будет $O(n)$ . Однако в среднем случае, когда дерево относительно ветвисто, сложность равна $O(\log n)$ .

*Рисунок 8. Вырождение BST при разном порядке вставки*

5.3. Сбалансированные BST

Описанная ранее проблема вырождения зависит от порядка вставки элементов, причём неудачный порядок характеризуется чёткой закономерностью: монотонной упорядоченностью или чередованием элементов убывающей и возрастающей последовательностей. Это делает такую ситуацию вполне вероятной, если в самом источнике данных присутствуют соответствующие статистические закономерности. Потому простейшим способом немного снизить вероятность такой ситуации является вставка элементов в случайном порядке, если это возможно. Однако надёжное решение проблемы вырождения заключается в использовании сбалансированных или самобалансирующихся деревьев.

Сбалансированным принято называть дерево, в котором высота не превышает оценки $O(\log n)$ . Это гарантирует, что все основные операции будут выполняться за $O(\log n)$ . Различные структуры достигают этого разными путями и само понятие сбалансированности в их узком смысле может различаться.

Классический пример сбалансированного дерева – AVL-дерево. Это модификация BST, в которой гарантируется сбалансированность в довольно жёстком смысле: высота левого и правого поддерева любого узла отличаются не более, чем на 1. Достигается это за счёт выполнения специальных операций поворота при каждой вставке или удалении.

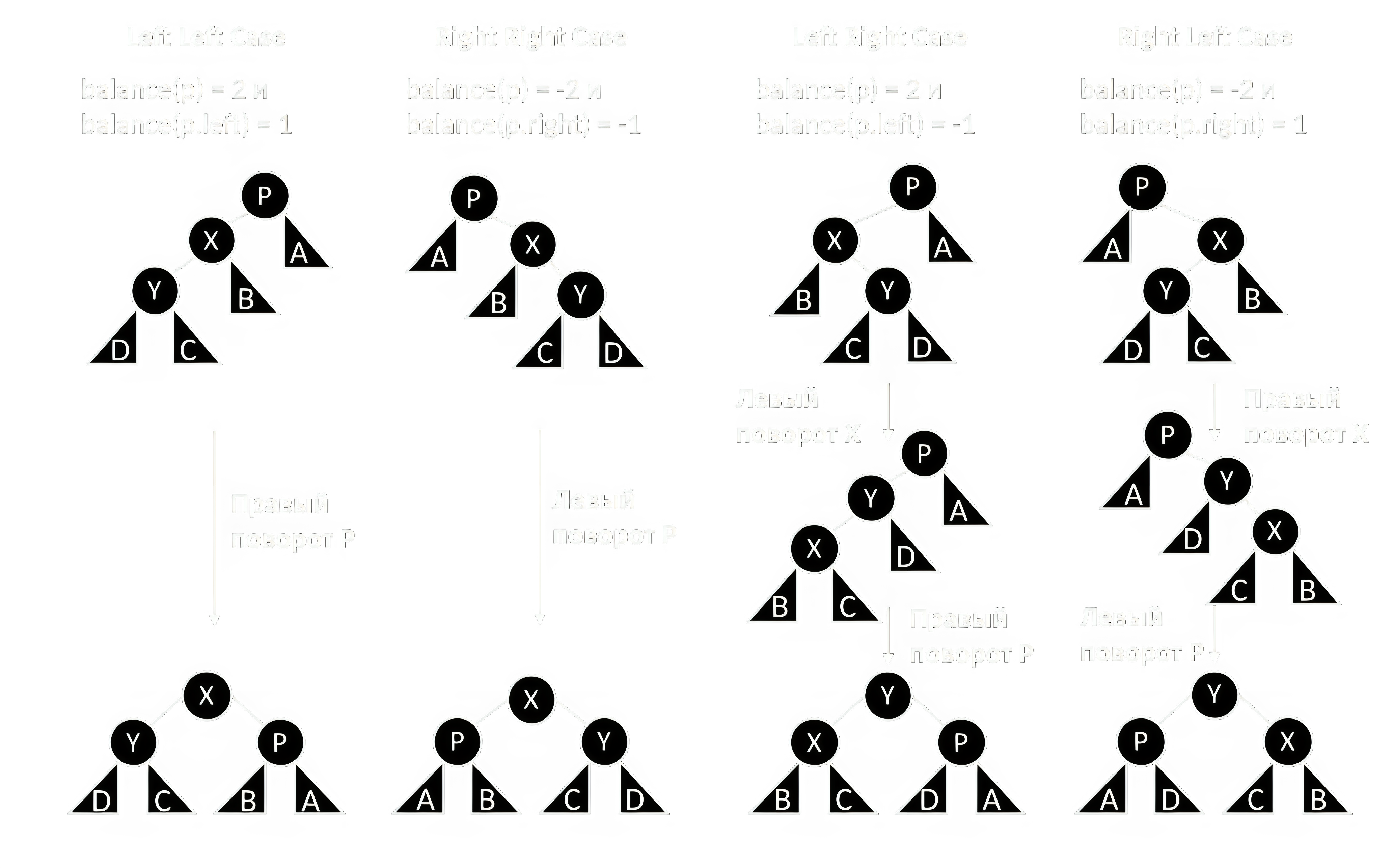
Различают два одинарных (левый и правый) и два двойных (лево-правый и право-левый) вида поворота. В результате левого поворота относительно узла $P$ его правый сын ( $R$ ) становится новым корнем поддерева, $P$ становится левым сыном $R$ , а левый сын $R$ становится правым сыном $P$ . Правый поворот является симметричным отражением этого случая. Двойной лево-правый поворот сводится к левому повороту относительно левого сына ( $L$ ) и затем правому повороту относительно $P$ . Право-левый поворот также является симметричным отражением предыдущего, состоя из правого поворота относительно правого сына ( $R$ ) и затем левого поворота относительно $P$ . Все операции поворота имеют константную сложность. Псевдокод левого и лево-правого поворота приведён в листинге:

def rotate_left(root):
    right = root.right
    root.right = right.left
    if root.right is not None:
        root.right.parent = root
    right.left = root
    right.parent = root.parent
    root.parent = right
    return right

def rotate_left_right(root):
    root.left = rotate_left(root.left)
    return rotate_right(root)

Обозначим функцией balance(p) разницу высот левого и правого поддерева узла $p$ . Эту величину называют коэффициентом сбалансированности (balance factor). В сбалансированном AVL дереве он равен -1, 0 или 1. При вставке нового значения может произойти нарушение балансировки и коэффициент одного из узлов изменится на 2 или -2. Правила применения поворотов для этого узла изображены на рисунке 9.

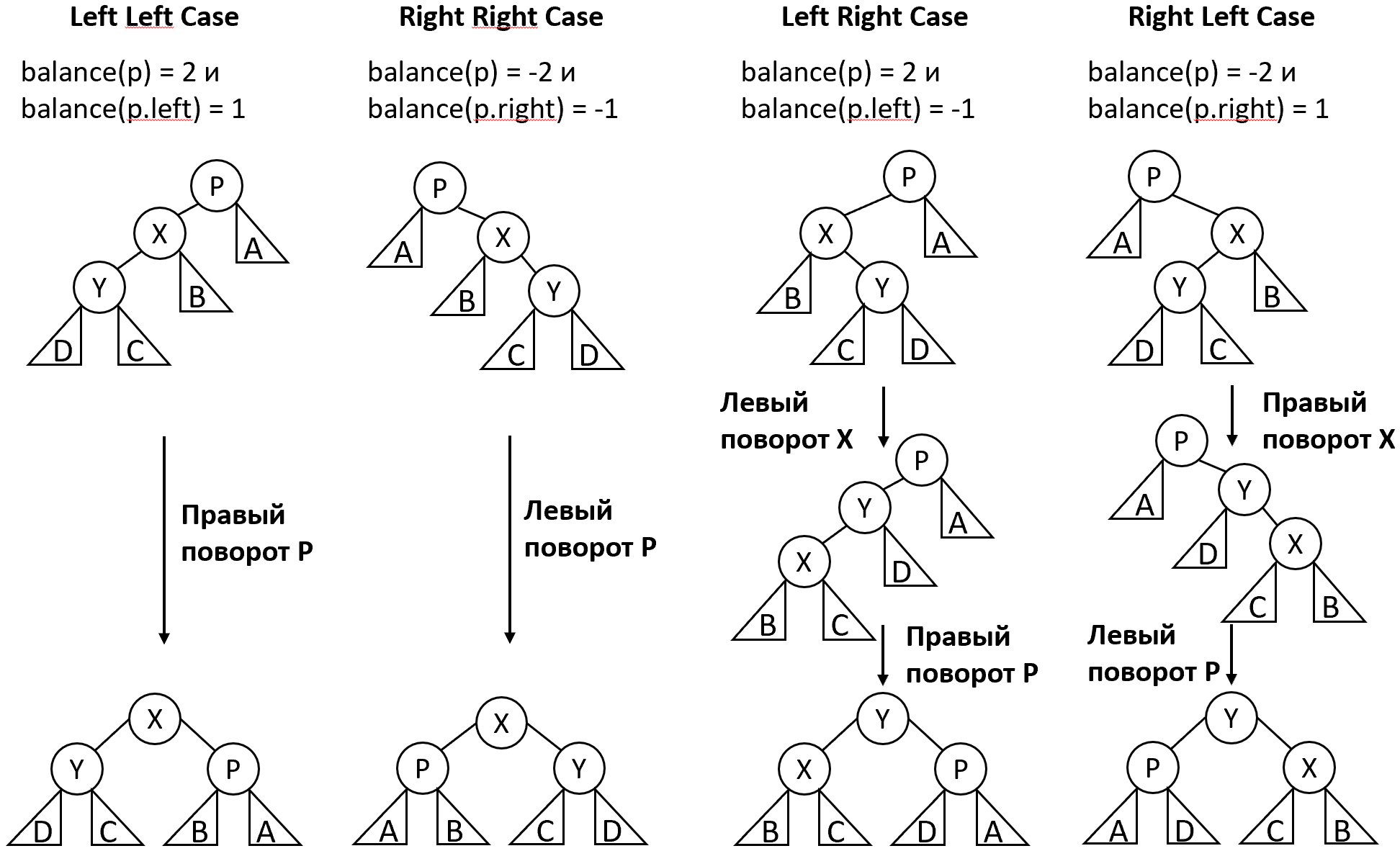
Вставка и удаление в AVL-дереве осуществляются сперва точно так же, как в BST, но затем может потребоваться перебалансировка узлов в цепочке родителей вставленного или удалённого. Таким образом, максимальное количество поворотов равно высоте дерева, т.е. $O(\log n)$ .

AVL-дерево на практике практически не используется. Всё дело в том, что слишком жёсткое требование сбалансированности ведёт к большим накладным расходам: необходимость перебалансировки возникает слишком часто. Но концепцию поворотов используют многие другие структуры данных, в том числе наиболее употребимая на практике вариация BST – красно-чёрное дерево.

Красно-чёрное дерево (Red-Black Tree, RBT) – это модификация BST, в которой каждому узлу соответствует один из двух цветов: красный или чёрный. Под цветом здесь понимается лишь некая условная метка. Также добавляются вспомогательные листовые Nil-узлы так, что любой значащий узел технически всегда имеет двух потомков, но от 0 до 2 из них могут быть Nil-узлами, олицетворяя отсутствие значения. На практике не нужно создавать много экземпляров подобного узла в памяти, достаточно указывать ссылки на один и тот же единственный Nil-узел.

В красно-чёрном дереве выполняются следующие свойства:

Каждый узел либо красный, либо чёрный;
Корень всегда чёрный;
Все листья (Nil-узлы) считаются чёрными;
У красного узла оба дочерних узла – чёрные;
Любой путь от узла до листьев, являющихся его потомками, содержит одинаковое количество чёрных узлов (чёрная высота).

Выполнение этих свойств связано с гарантией сбалансированности следующим образом. Пусть в дереве с чёрной высотой $h_b$ нет красных узлов, тогда из свойств 3 и 5 оно будет полным. Количество узлов в полном дереве равно $2^{h_b} - 1$ . Значит в произвольном дереве с той же чёрной высотой общее число узлов $n \ge 2^{h_b} - 1$ . Исходя из свойств 4 и 5, длиннейший путь представляет собой чередование красных и чёрных узлов и имеет длину $2h_b - 1$ . Следовательно, $h \le 2h_b - 1 = 2 \log_2 (n + 1) - 1 = O(\log n)$ .

Как и для AVL деревьев, вставка и удаление в RBT осуществляются сперва точно так же, как в BST, но затем может потребоваться перебалансировка и перекраска узлов для восстановления вышеперечисленных свойств.

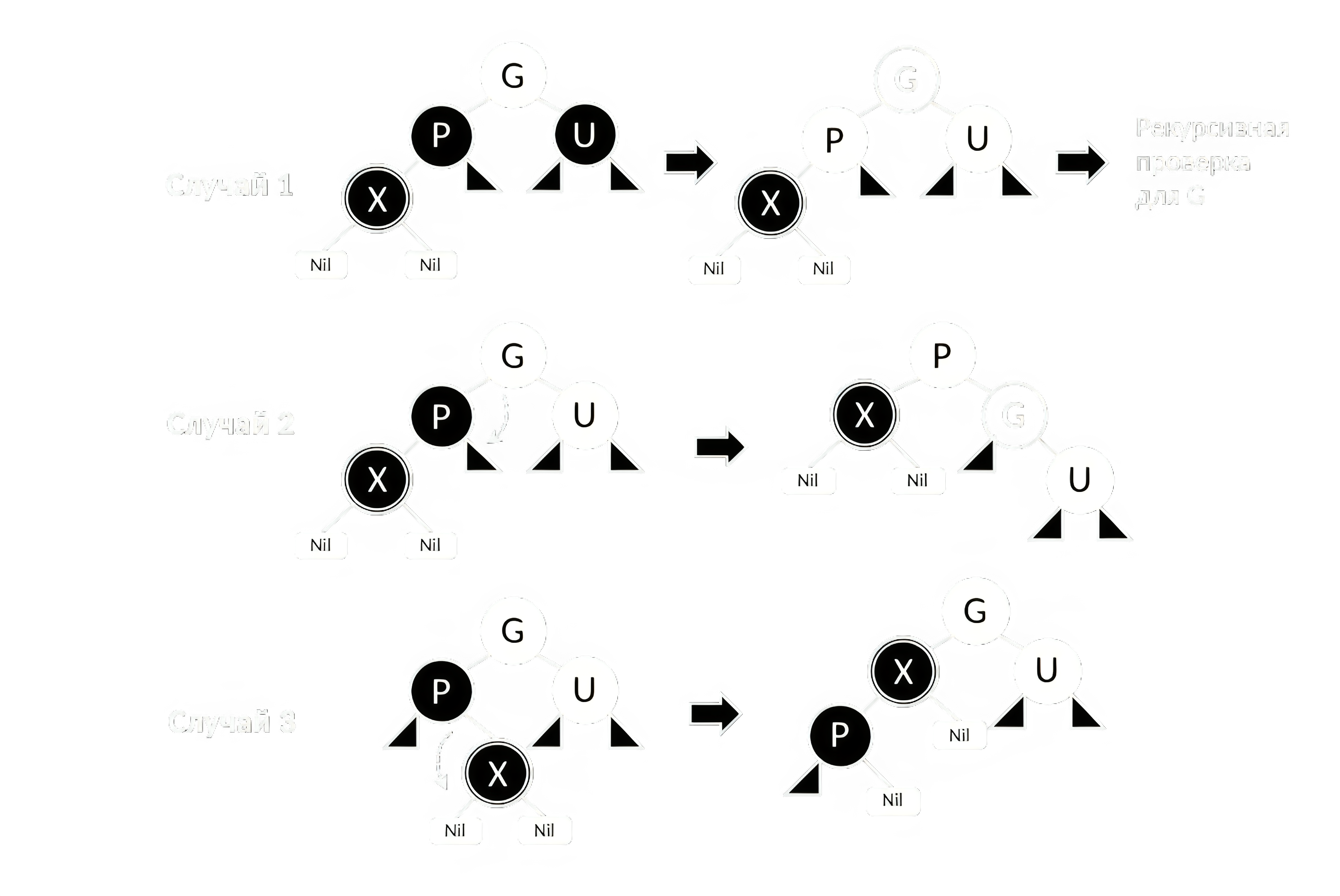
Предполагается, что новый узел изначально окрашен в красный. Потому после вставки может нарушиться свойство 2 или 4. Если дерево было пусто до вставки, то для исправления нарушения 2 свойства достаточно перекрасить корень в чёрный. Если родитель вставленного узла чёрный, то нарушений нет. Иначе возможны 3 случая нарушения свойства 4 (не считая зеркальные), изображённые на рисунке 10.

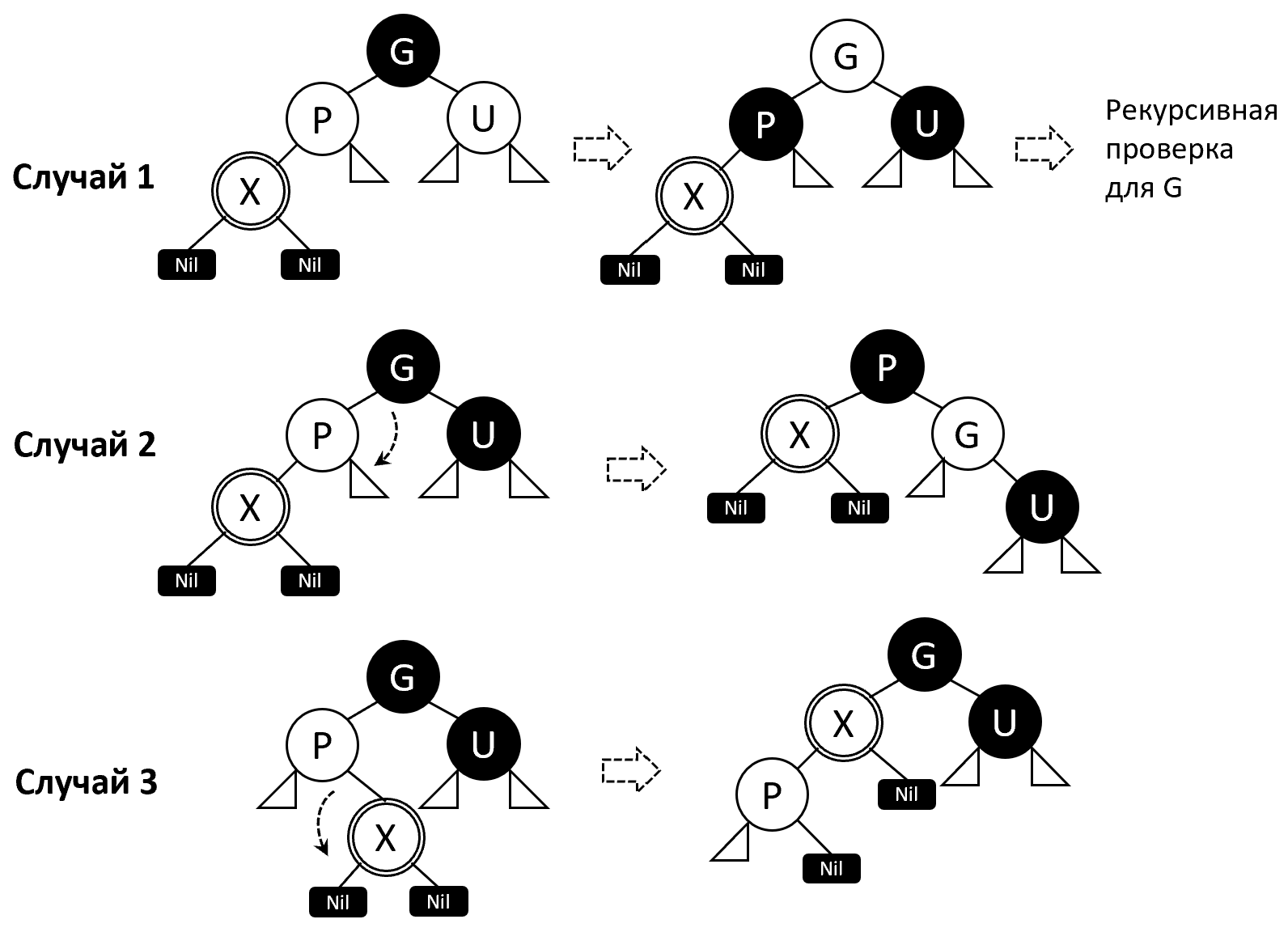
*Рисунок 10. Восстановление свойств RBT после вставки (3 основных случая)*

При удалении насчитывается ещё больше возможных случаев, но общий принцип остаётся тем же: если фиксируется нарушение свойств, необходимо выполнить повороты и перекраску узлов, а также, возможно, продолжать проверку, поднимаясь вверх.

На базе красно-чёрного дерева реализованы древовидные варианты словаря практически по всех стандартных библиотеках языков (SortedDictionary и SortedSet в C#, TreeMap и TreeSet в Java, std::map и std::set в C++). Оно применяется повсеместно для самых различных задач. Менее жёсткий подход к сбалансированности (гарантируется различие длин путей не более чем в 2 раза) приводит к меньшим накладным расходам, что делает его отличным выбором для динамично меняющихся данных.

5.4. Хеш-таблицы

Хеш-таблицы (Hash Table, Hash Map) отражают принципиально другой подход к реализации словаря, пытаясь воплотить идею таблиц прямого доступа: что если по ключу можно было бы сразу определить местоположение соответствующего значения. Точно так же, как с операцией индексации в массиве. Для этого необходимо ввести отображение ключей на индексы обычного массива, которое называется хеш-функцией.

Т.к. область значений ключа (пространство ключей) всегда намного шире, чем область значений индекса (пространство записей), то хеш-функция может ставить в соответствие разным ключам один и тот же индекс. Такая ситуация называется коллизией. Хорошая хеш-функция должна стремиться к равномерному распределению ключей по индексам, чтобы минимизировать число коллизий. Среди прочих требований к хеш-функции можно выделить следующие:

скорость вычисления (обычно используются быстрые побитовых операции);
детерминированность;
сложность не должна зависеть от числа элементов (только от длины ключа);
связь между входными значениями не должна отображаться в связь между выходными.

В общем случае результат хеш-функции называют хешем (или хеш-кодом). И сам приём хеширования применяется во многих других областях: криптографии, сжатии данных, проверки целостности, идентификации и распознавании объектов и т.д. Хеш – это просто некая последовательность байт, которую в случае хеш-таблиц можно привести к целому типу, интерпретируя как индекс в массиве. При этом нужно учитывать возможность выхода за границы массива и делать hash % h, где $h$ – размер массива.

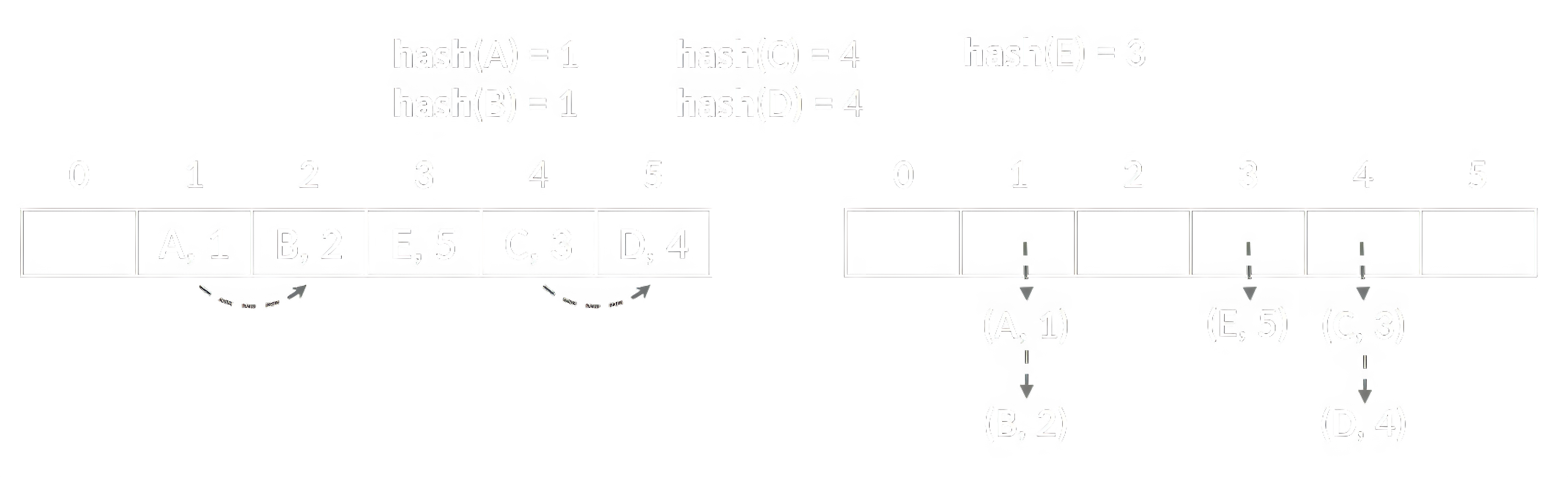
Существует 2 основных способа разрешения коллизий: метод цепочек и метод открытой адресации (рисунок 11). При методе цепочек каждая ячейка массива содержит указатель на связный список, в котором накапливаются пары ключ-значение, по которым происходили соответствующие коллизии. Тогда основные операции сводятся к следующему:

Lookup (поиск): вычисляем хеш ключа, получаем индекс, переходим по указателю в список и линейно ищем пару с нужным ключом;
Insert (вставка): ищем по ключу, если нашли, то обновляем значение, иначе добавляем новую пару в список;
Delete (удаление): ищем по ключу, если нашли, то удаляем пару из списка.

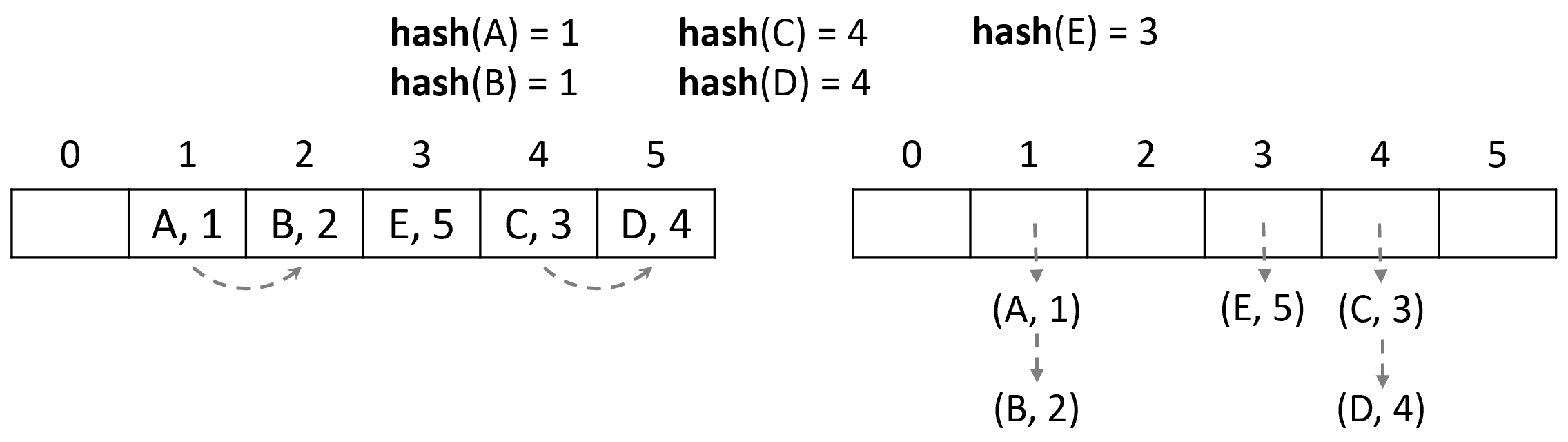
Методы разрешения коллизий в хеш-таблицах: открытая адресация и метод цепочек — *Рисунок 11. Методы разрешения коллизий в хеш-таблицах: открытая адресация (слева) и метод цепочек (справа)*

Вместо связного списка при высокой заполненности отдельных ячеек можно использовать красно-чёрное дерево, что ускорит поиск.

Метод открытой адресации предполагает хранение в каждой ячейке массива не более одной пары ключ-значение. Для этого при коллизии ищется другая свободная ячейка. Существуют различные стратегии поиска свободной ячейки, начиная с указанной: линейная (с фиксированным шагом), квадратичная (с экспоненциально растущим шагом) и другие. Отдельную сложность создаёт проблема выхода за границы массива в процессе поиска. Обычно это решается циклическим обходом с возможным сдвигом, если требуется (чтобы не обходить ровно те же позиции).

При поиске, если ключ в ячейке не совпадает с искомым, необходимо ровно тем же алгоритмом, что используется при вставке, обходить ячейки до тех пор, пока не будет найдена нужная пара или пустая ячейка (это означает, что пары с таким ключом нет). Таким образом, коллизия в методе открытой адресации точно так же приводит к необходимости поиска в подпоследовательности пар, по которым она происходила. Только здесь эта подпоследовательность не помещена в отдельный список, а объединена неявно алгоритмом обхода.

Несколько сложнее при открытой адресации реализуется удаление. Нельзя просто затереть ячейку, т.к. это разрежет подпоследовательность и может привести к потере данных. Поэтому при удалении соответствующая ячейка помечается как удалённая, но не очищается. При поиске такая ячейка не воспринимается как конец подпоследовательности, а при вставке она может быть перезаписана.

При выборе метода разрешения коллизий нужно учитывать их особенности. В частности, метод цепочек позволяет вмещать неограниченное число элементов и сохраняет неизменными указатели на хранимые объекты, но требует дополнительных затрат по памяти на указатели в списках. В свою очередь, при методе открытой адресации гораздо эффективнее используется процессорный кеш, но из-за переполнения необходимо периодическое перевыделение памяти с переносом всех элементов, а также скорость резко деградирует при высокой заполненности. На практике чаще применяется метод открытой адресации.

Основные операции в хеш-таблицах (вставка, поиск, удаление) имеют амортизационную сложность $O(1)$ в среднем случае. Однако в худшем случае, когда все ключи хешируются в один индекс, сложность становится $O(n)$ . Поэтому критичен выбор качественной хеш-функции и динамическое изменение размеров по необходимости, чтобы держать массив в пределах определённого уровня заполненности.

На базе хеш-таблиц реализованы словари практически во всех стандартных библиотеках языков:

Java – HashMap, HashSet, LinkedHashSet, LinkedHashMap;
C# – Dictionary, Hashtable, HashSet;
C++ – unordered_map, unordered_set;
Python – dict, set;
Ruby – Hash.

Благодаря амортизационной константной сложности хеш-таблицы в целом предпочтительнее для многих задач по сравнению с древовидными реализациями словаря. Однако они не годятся там, где нужен упорядоченный обход или поиск по диапазону. Кроме того, сбалансированные деревья дают гарантию $\log n$ сложности, в то время как хеш-таблицы теоретически могут выродиться в $O(n)$ .

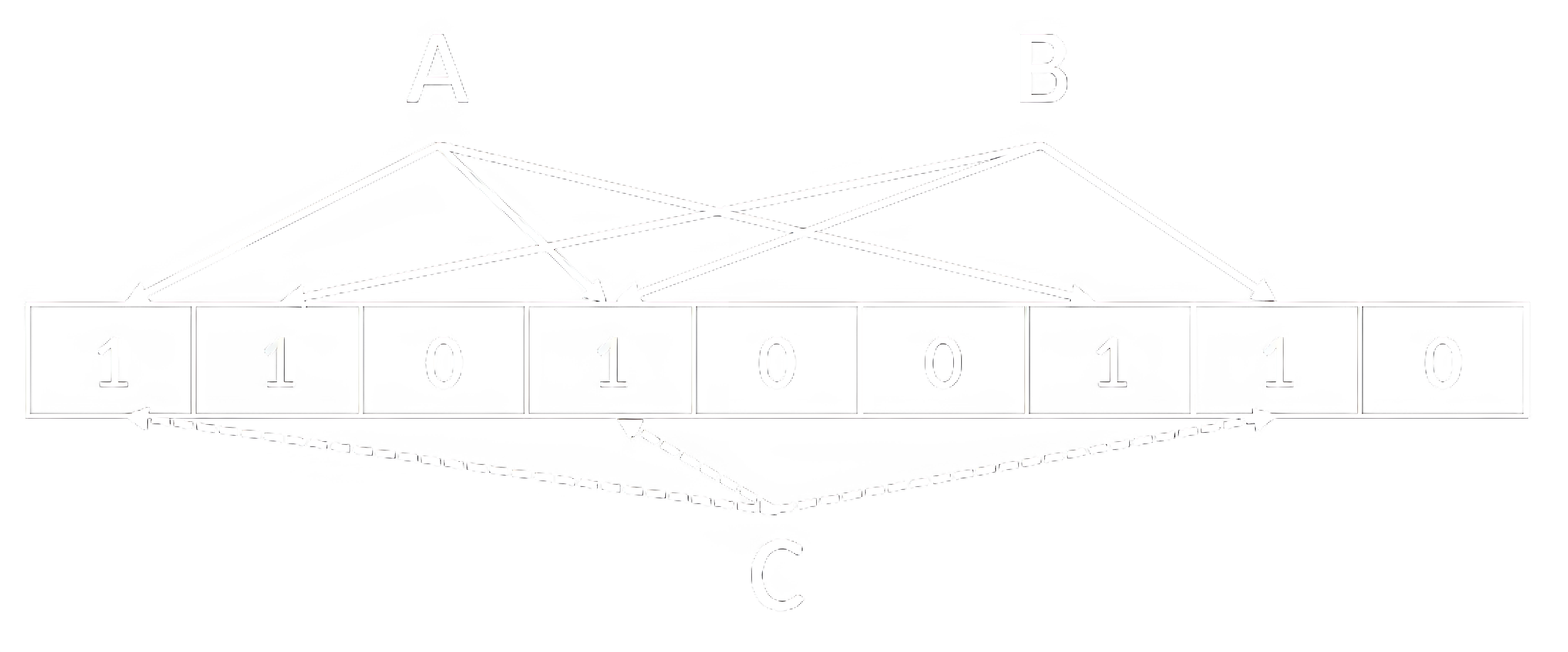
Для компактного представления множеств в определённых ситуациях применяется также вероятностная структура данных на базе хеширования, которая называется фильтром Блума (Bloom Filter). Она представима битовой маской фиксированного размера и набором хеш-функций (рисунок 12). Для добавления ключа в множество вычисляются значения всех хеш-функций, и соответствующие биты в маске устанавливаются в 1. Для проверки наличия элемента вычисляются значения тех же хеш-функций, и если хотя бы один из соответствующих битов не установлен, то элемента в множестве нет. Такой принцип допускает ложноположительные результаты (в силу коллизий), но не ложноотрицательные. Ниша для применения такой специфической структуры данных – увеличение эффективности различных систем путём первоначальной беглой проверки, при отрицательном результате которой можно не тратить основные ресурсы.

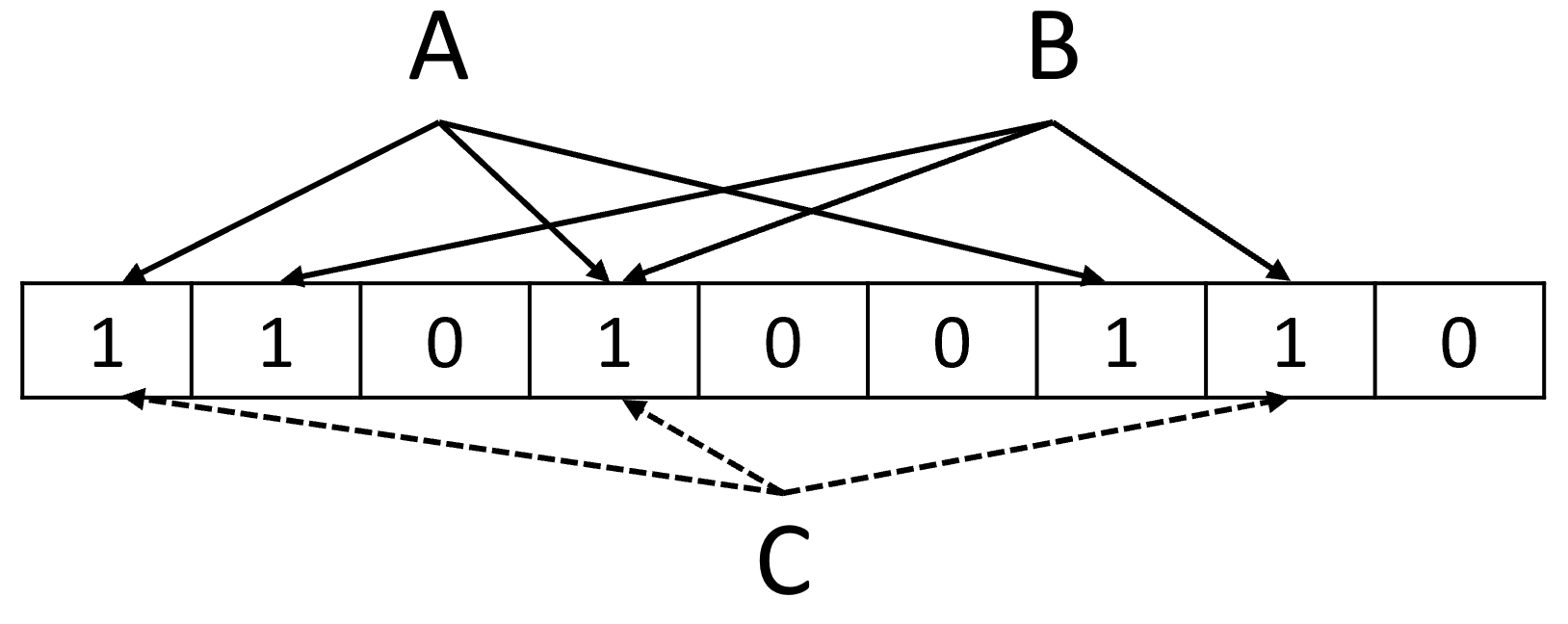
Примеры применения фильтра Блума:

оптимизация кеширования за счёт игнорирования разовых запросов (one-hit wonders);
оптимизация проверки наличия записей в базе данных;
оптимизация проверки наличия записей в белых/чёрных списках.

5.5. Префиксное дерево

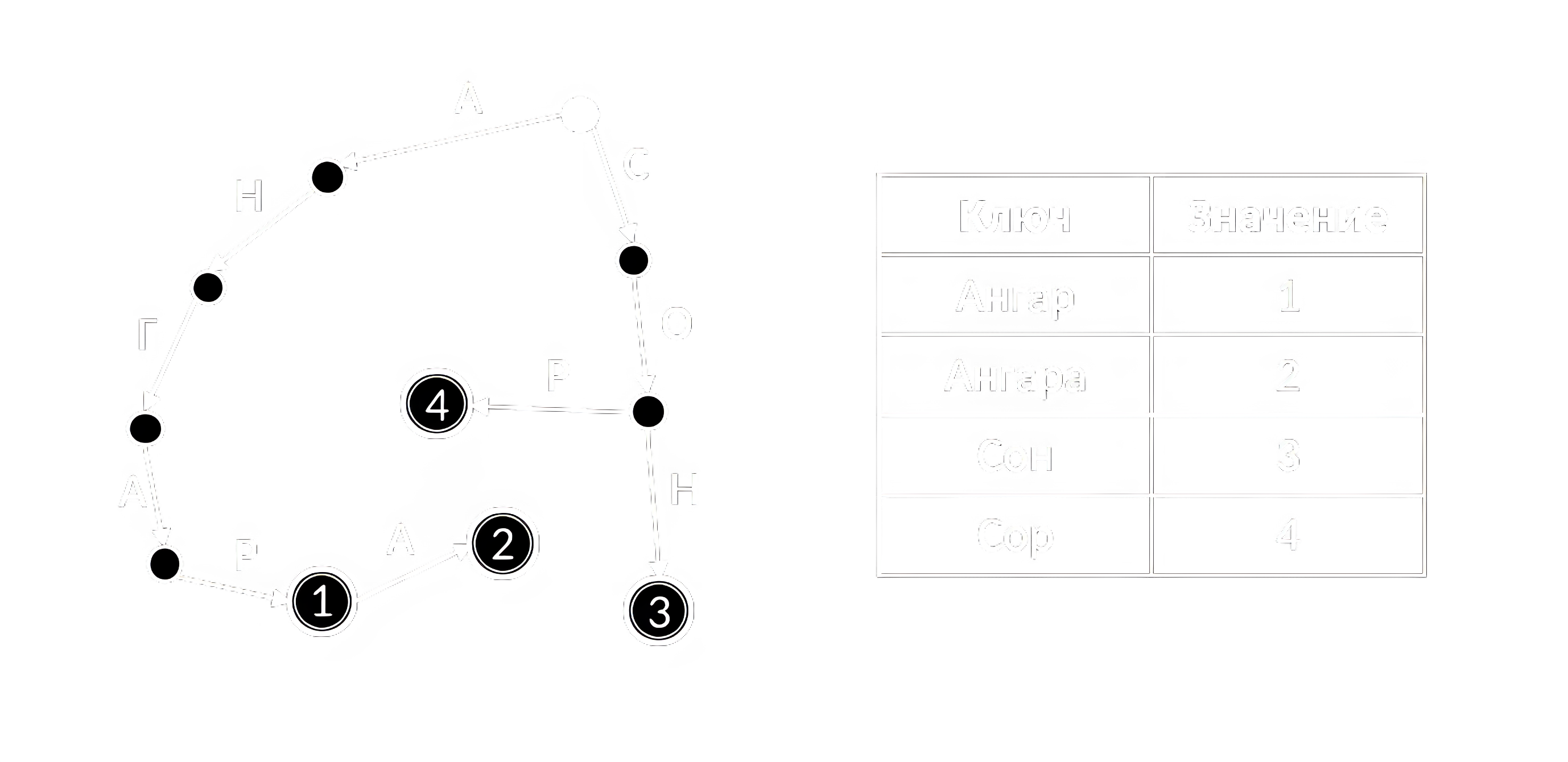
Префиксное дерево (бор, Trie, Prefix Tree) качественно отличается от прочих вариантов реализации словаря. Хоть оно и поддерживает тот же интерфейс и может использоваться вместо красно-чёрного дерева или хеш-таблицы, но, как правило, не эффективно в этой роли. Сферы его применения лежат там, где ключи представимы как последовательность составных частей (символов, слогов, морфем, и т.д.), и требуется поиск, учитывающий подобную структуризацию. Особенно эффективно реализуется операция поиска по префиксу, когда требуется найти все ключи, начинающиеся с заданной последовательности.

Пусть задан алфавит $A = \{a_1, a_2, \ldots, a_d\}$ . Каждый ключ представим как конечную последовательность символов этого алфавита: $key = a_{i_1}a_{i_2}\ldots a_{i_m}$ . Тогда внутренний узел может иметь до $d$ дочерних узлов, и связь с каждым соответствует одному из символов алфавита. Ключи не хранятся в явном виде, а закладываются в структуру префиксного дерева. Корень дерева соответствует пустой строке, внутренние узлы – различным префиксам, присутствующим у ключей. Для указания на листовые узлы со значениями можно завести вспомогательный символ, не принадлежащий алфавиту $A$ . Альтернативно, можно завести в структуре узла флаг is_end и поле value, тогда значения будут храниться в развилочных узлах. При последнем подходе не требуется лишний узел на каждый ключ, но возникают затраты памяти на дополнительные поля. Далее будем предполагать именно подобную техническую реализацию.

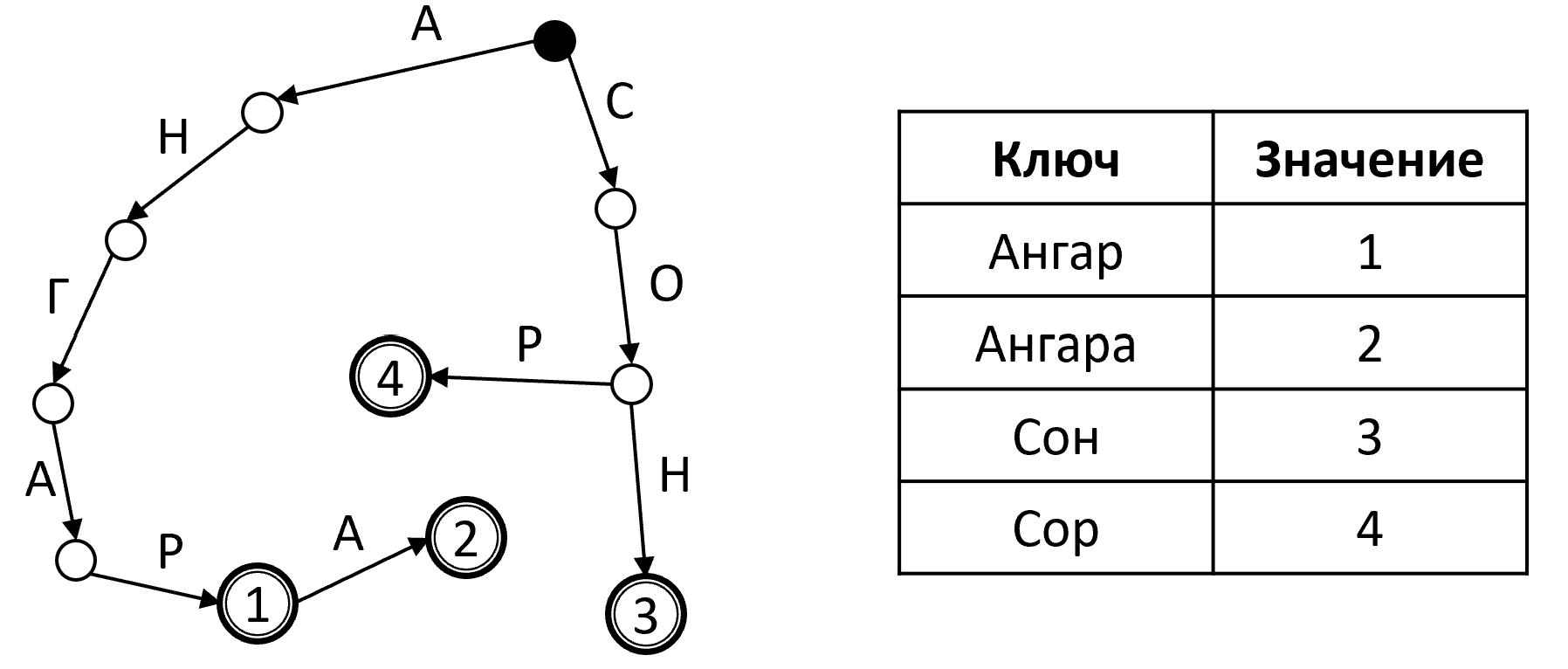
Каждый узел префиксного дерева хранит информацию о дочерних связях во внутренней структуре словаря с символами-ключами и значениями-указателями на узлы детей. Для абстрагирования от деталей реализации введём операции get_child(c) (получение ребёнка по символу $c$ ), set_child(c, node) (установка ребёнка по символу $c$ ), remove_child(c) (удаление ребёнка по символу $c$ ). При использовании статического массива (каждая ячейка соответствует одному символу алфавита) получим сложность $O(1)$ , при связном списке пар – $O(d)$ , при хеш-таблице – $O(1)$ в среднем случае, при красно-чёрном дереве – $O(\log d)$ . На выбор влияет размер алфавита, требования по памяти и быстродействию и другие факторы.

Приведём псевдокод основных операций на префиксном дереве. Для получения значения по ключу необходимо спускаться, двигаясь по ссылкам, соответствующим очередному символу искомого ключа. Если последний узел является листом, то в нём содержится значение. Если на каком-то шаге мы не находим нужного ребёнка, значит ключа в дереве нет. Сложность операции – $O(m \cdot T(get\_child))$ , где $m$ – длина ключа.

def trie_search(root, key):
    node = root
    for c in key:
        node = node.get_child(c)
        if node is None:
            return None
    if node.is_end:
        return node.value
    return None

Вставка осуществляется схожим образом, только при отсутствии очередной ветви она создаётся на ходу, а в конечном листе устанавливается значение. Сложность операции в худшем случае – $O(m \cdot (T(set\_child) + T(get\_child)))$ .

def trie_insert(root, key, value):
    node = root
    for c in key:
        child = node.get_child(c)
        if child is None:
            child = TrieNode()
            node.set_child(c, child)
        node = child
    node.value = value
    node.is_end = True

При удалении ключа может образоваться ветвь, не ведущая к листьям и больше не соответствующая какому-либо префиксу. Её необходимо подчистить. Сложность – $O(m \cdot (T(remove\_child) + T(get\_child)))$ .

def trie_delete(root, key):
    node = root
    for c in key:
        node = node.get_child(c)
        if node is None:
            return
    node.value = None
    node.is_end = False
    while node != root and len(node.children) == 0 and not node.is_end:
        parent = node.parent
        parent.remove_child(node)
        node = parent

Вышеуказанные операции позволяют имплементировать интерфейс словаря. В довесок к этому на префиксном дереве эффективно реализуются специфичные задачи, трудно решаемые на других структурах. В частности, для получения всех ключей, начинающихся с заданного префикса, достаточно спуститься в узел, соответствующий этому префиксу, и обойти поддерево с ним в корне. Все достижимые листовые узлы будут соответствовать искомым ключам.

Другой пример – поиск опечаток в словах. Для этого префиксное дерево обходится рекурсивно, накапливая независимо в каждой ветви обхода счётчик ошибок (несоответствий текущего префикса ключу). Дальнейшее рекурсивное углубление по ветви прекращается, когда счётчик ошибок превышает допустимое значение. При должной реализации этот подход позволяет учитывать возможность указания ошибочного символа, пропуска символа, наличие лишнего.

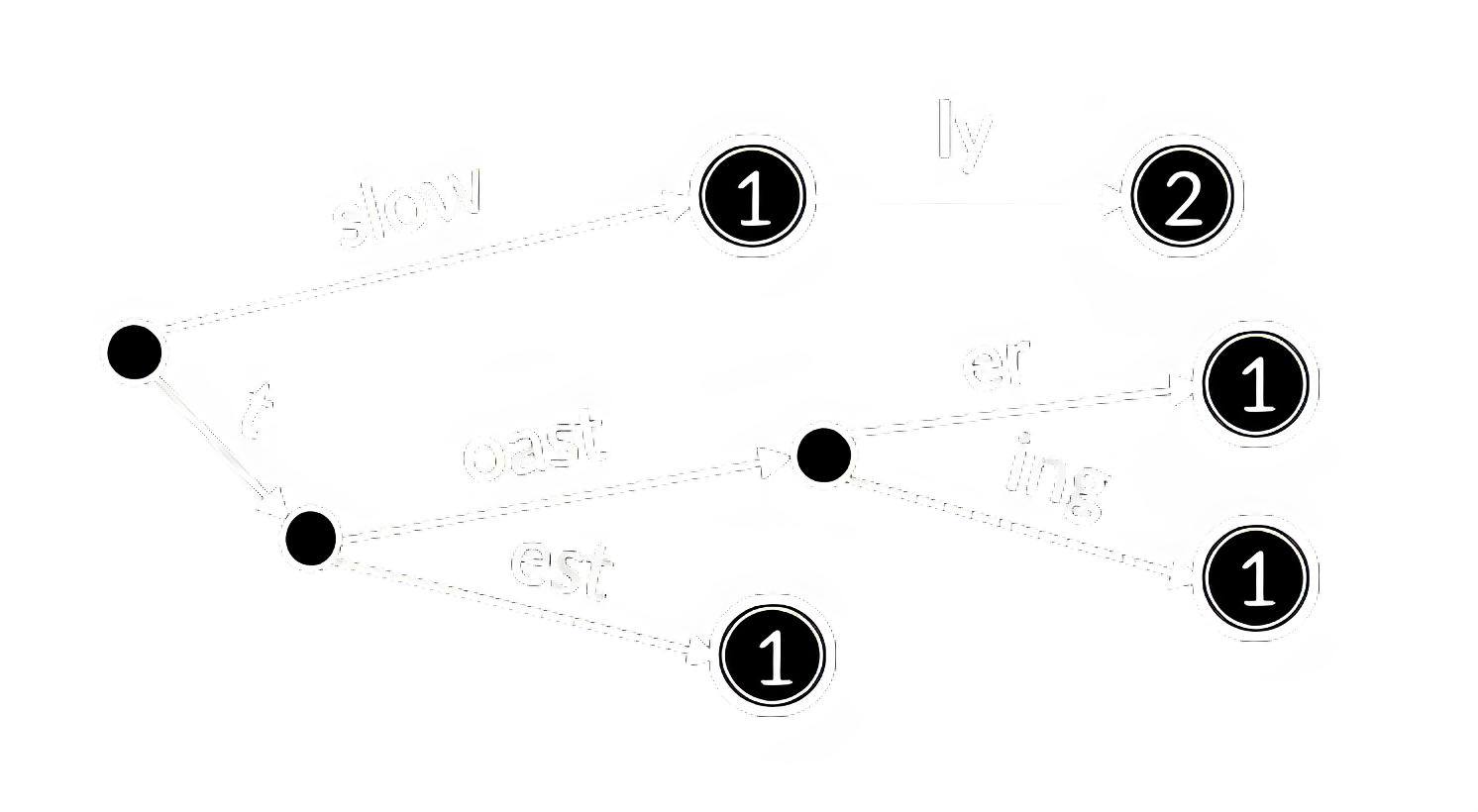
У префиксного дерева есть ряд модификаций. Во-первых, стоит заметить, что любые данные могут кодироваться строкой бит, а значит храниться в префиксном дереве. Такой вариант с сиволами 0 и 1 называется Bitwise Trie. Чем больше в множестве строк, помещённых в префиксное дерево, совпадений префиксов, тем эффективнее переиспользование существующих узлов. Однако для разрежённого словаря данная структура может быть крайне избыточной по памяти. Для борьбы с этим недостатком можно сжимать линейные цепочки узлов, объединяя их в один. Тогда рёбрам дерева будут соответствовать не отдельные символы алфавита, а целые последовательности. Такая сжатая модификация называется базисым деревом (Compressed Trie, Radix Tree) (рисунок 14). В ряде задач требуется искать ключи не по совпадению префикса, а по совпадению суффикса. Вариант сжатого дерева, где ключи обходятся в обратном порядке, а узлы соответствуют суффиксам, называется суффиксным деревом (Suffix Tree).

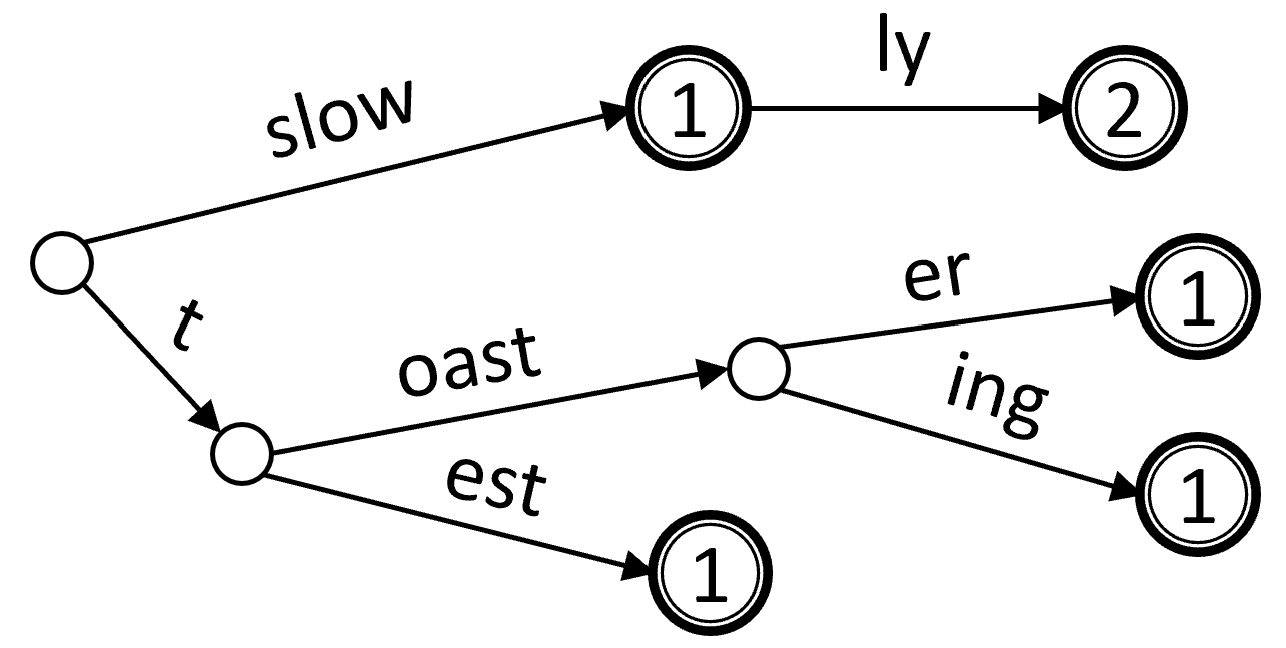
*Рисунок 14. Сжатое префиксное дерево (Radix Tree)*

Вот лишь некоторые задачи, для решения которых могут применяться префиксные деревья и их модификации:

автодополнение (IntelliSense в редакторах кода, Google Suggest);
поиск маршрута по IP-адресу (Cisco, Juniper, BIRD, FRRouting);
сжатие данных (LZ78, LZW);
обработка ДНК/белковых последовательностей (BLAST, Bowtie, BWA);
расстановка переносов;
исправление опечаток.

5.6. Прочие реализации

Среди прочих реализаций словаря стоит отдельно выделить B-дерево (B-tree). Это дерево произвольной ветвистости, причём обычно очень высокой.

Основные характеристики B-дерева:

Каждый узел может содержать множество ключей, ключи хранятся в отсортированном порядке;
Количество ключей в узле лежит в пределах $[d, 2d - 1]$ (кроме корня при незаполненности), где $d$ – минимальная степень дерева;
Количество детей узла равно количеству ключей узла + 1, причём ключи являются разделителями: если $k_i$ – произвольный ключ в поддереве $i$ -го ребёнка, а $key_i$ – $i$ -й ключ в узле (из $m$ ), то

k_1 \leq key_1 \leq k_2 \leq ... \leq k_{m} \leq key_{m} \leq k_{m+1}; \tag{11}

Высота дерева не превосходит $O(\log n)$ ;
Все листья расположены на одной глубине.

В отличие от многих других деревьев, B-дерево растёт вверх, а не вниз. Для выполнения ограничений на количество ключей при вставке и удалении может потребоваться объединение или разбиение узлов. При разбиении в родителя на соответствующую позицию выносится ключ-разделитель (обычно медианный элемент). Если происходит разделение корня, то дерево вырастает вверх на 1 уровень, т.к. необходимо создать новый корень, куда помещается ключ-разделитель.

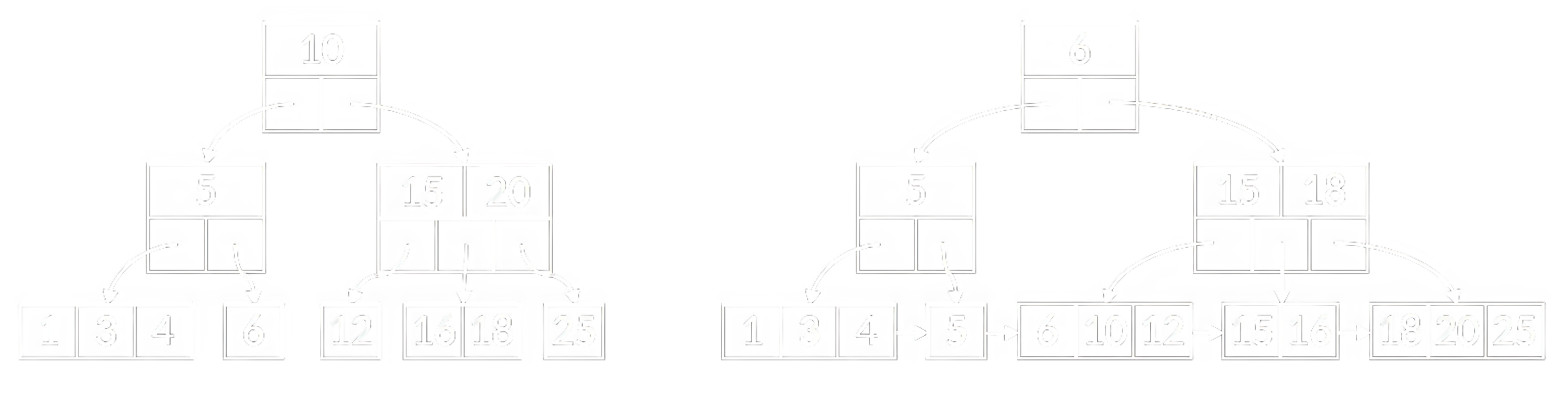
Сами по себе B-деревья не столь популярны, однако иное можно сказать о модификации, называемой B+ дерево. В B+ дереве все пары ключ-значение хранятся в листьях, а внутренние узлы содержат только навигационные ключи – копии ключей из листьев. На рисунке 15 изображены B и B+ деревья, построенные на одном и том же наборе данных. Все узлы листового уровня в B+ дереве по сути представляют собой упорядоченный связный список пар, над которым выстроены поверхностные уровни для эффективного поиска. Это упрощает получение элементов, попадающих в диапазон: достаточно найти первый элемент, а затем последовательно перебирать все следующие по цепочке до достижения верхней границы диапазона. Кроме того, отсутствие значений во внутренних узлах делает их компактнее, что позволяет уместить больше ключей на одном дисковом блоке и строить более ветвистые и низкие деревья. Производительность B+ деревьев предсказуемее, т.к. всегда необходим проход от корня до листа.

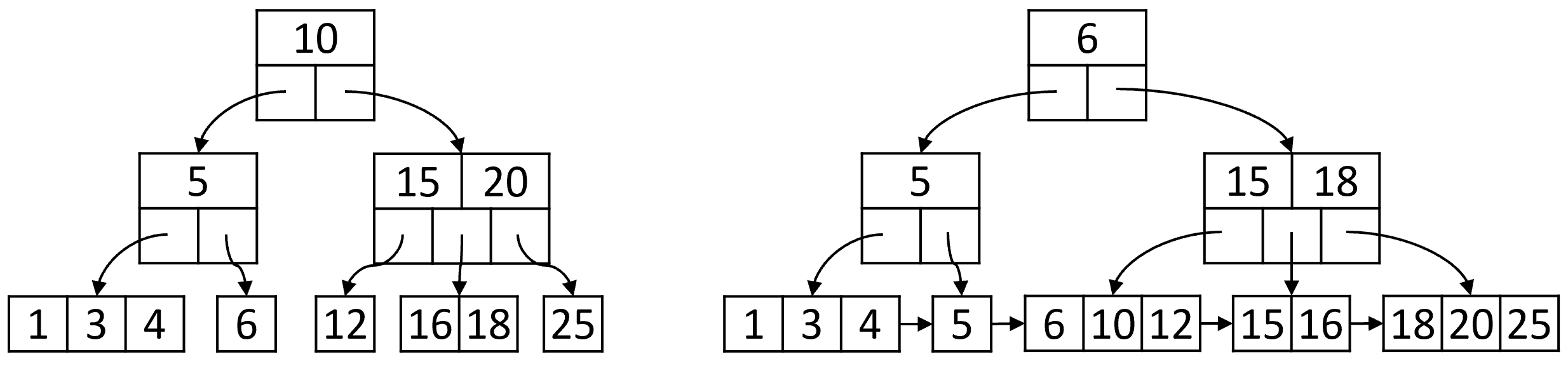
B+ дерево широко применяется в системах управления базами данных для реализации индексов общего назначения. Всё благодаря тому, что оно позволяет организовать поиск по данным огромных масштабов, считывая необходимую информацию с диска по частям и минимизируя количество таких операций. При этом сильно упрощаются поисковые запросы по диапазону ключей, а также получение упорядоченного списка элементов. Для нахождения всех элементов, чей ключ попадает в заданный диапазон, достаточно выполнить поиск по его левой границе, а затем двигаться по списку листового уровня до тех пор, пока ключ очередного элемента не превысит правую границу.

B+ деревья используются во всех популярных реляционных (и не только) СУБД: MySQL, PostgreSQL, Oracle и др. Кроме того, B+ деревья используются в различных файловых системах (NTFS, ext4, XFS), нереляционных СУБД (Neo4j, MongoDB), прокси-серверах (Varnish, Squid) и других приложениях.

Среди модификаций бинарного дерева поиска можно встретить косое дерево (Splay Tree). Оно старается реализовать концепцию того, что часто или недавно запрашиваемые значения эффективнее держать как можно ближе к корню дерева. Для этого после каждого доступа к узлу оно выполняет серию поворотов, чтобы переместить узел в корень. Данная структура имеет амортизированную сложность $O(\log n)$ для всех операций и не сталкивается с проблемой вырождения. Однако на практике косые деревья практически не используются, т.к. уступают прочим вариантам по многим значимым метрикам.

Ещё одну интересную концепцию реализации словаря можно встретить в виде списков с пропусками (Skip Lists). Эта структура является вероятностной и представляет собой многослойную структуру упорядоченных связных списков, в которой каждый верхний слой содержит подмножество элементов нижележащего. За счёт этого ли-нейный поиск по верхним слоям позволяет постепенно сужать диапазон по-иска, спускаясь вниз по уровням. Т.к. нижний слой представляет собой упо-рядоченный список всех элементов, то, как и в B+ дереве, легко и эффектив-но реализуется поиск по диапазону. Списки с пропусками относительно редки, но находят своё применение в ряде СУБД типа ключ-значение и не-которых других: Redis, LevelDB, RocksDB, Apache HBase, ClickHouse.

4. Очередь с приоритетом

6. Графы