3. Линейные структуры данных
3.1. Основные линейные структуры
Линейные структуры данных – это структуры, в которых элементы располагаются последовательно, друг за другом. Простейшей линейной структурой данных можно считать массив. О плюсах применения массивов как концепции последовательного размещения однородных элементов в памяти, уже было сказано ранее. Реализация даже относительно сложных структур на базе массива может быть крайне эффективной, особенно в случае доминирования операций чтения, т.к. индексация выполняется за . Однако любые изменения (вставка или удаление) в произвольной позиции имеют линейную сложность из-за необходимости смещения всех последующих элементов.
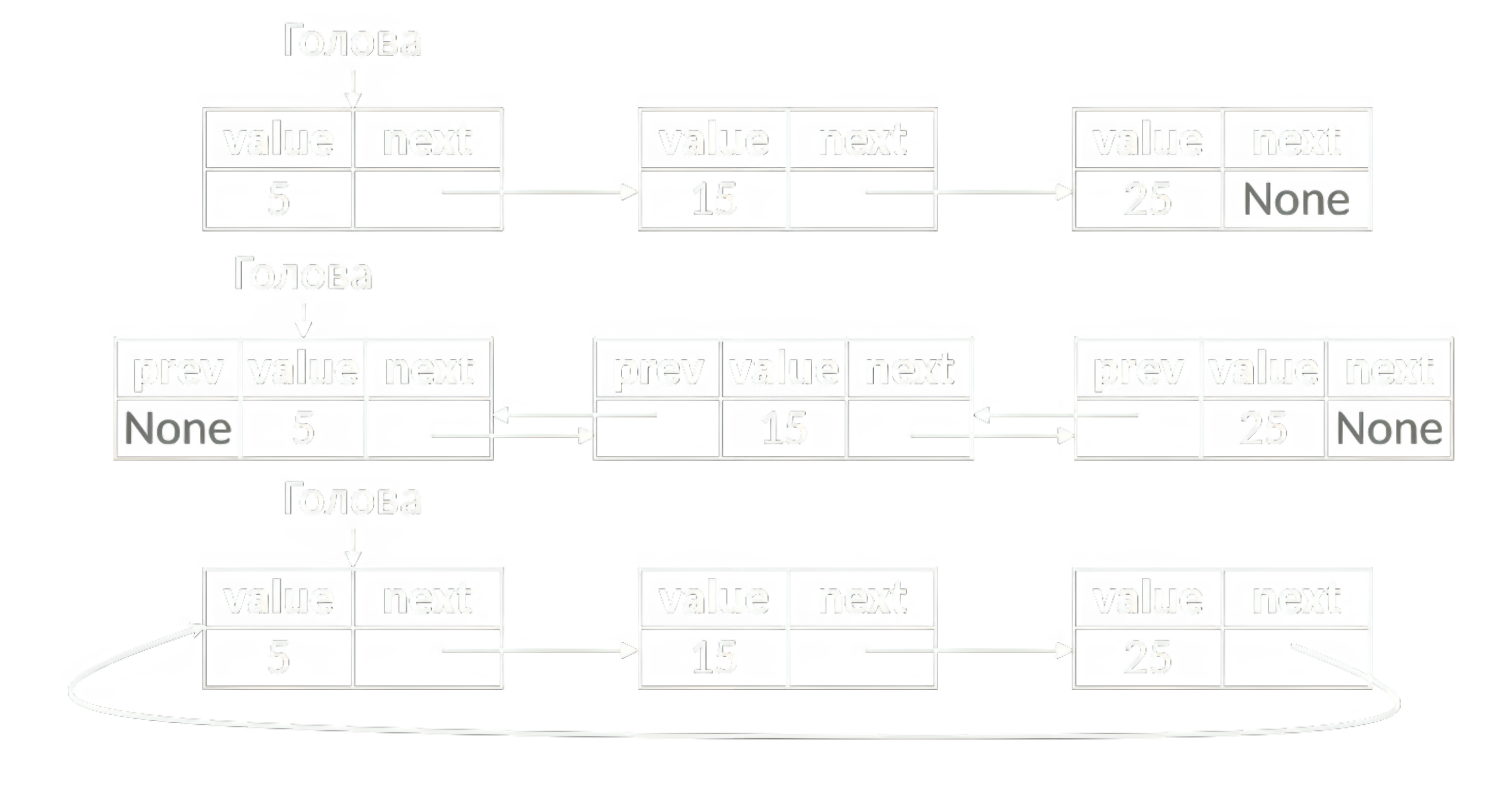
Альтернативой массиву служит связный список (Linked List). Он, напротив, обеспечивает константную сложность вставки или удаления элемента при наличии указателя на нужную позицию, но не позволяет произвольно обращаться к элементам по индексу – возможен только последовательный доступ. Его использование менее эффективно в плане задействования процессорного кеша, т.к. элементы могут располагаться далеко друг от друга в памяти. Кроме того, очистка памяти занимает , т.к. требует обхода и уничтожения каждого отдельного элемента. В то же время память под массив может быть освобождена за одну операцию при использовании низкоуровневых языков программирования и статического выделения памяти. Также связные списки менее эффективны по памяти, т.к. вместе с каждым элементом помимо самого значения хранится дополнительная информация в виде ссылок/указателей.
Различают односвязный и двусвязный список. В последнем каждый элемент хранит ссылку не только на последующий, но и на предыдущий, что позволяет перемещаться по списку в обоих направлениях. Кроме того, цепочку элементов можно замкнуть, получив кольцевой список (рисунок 2).
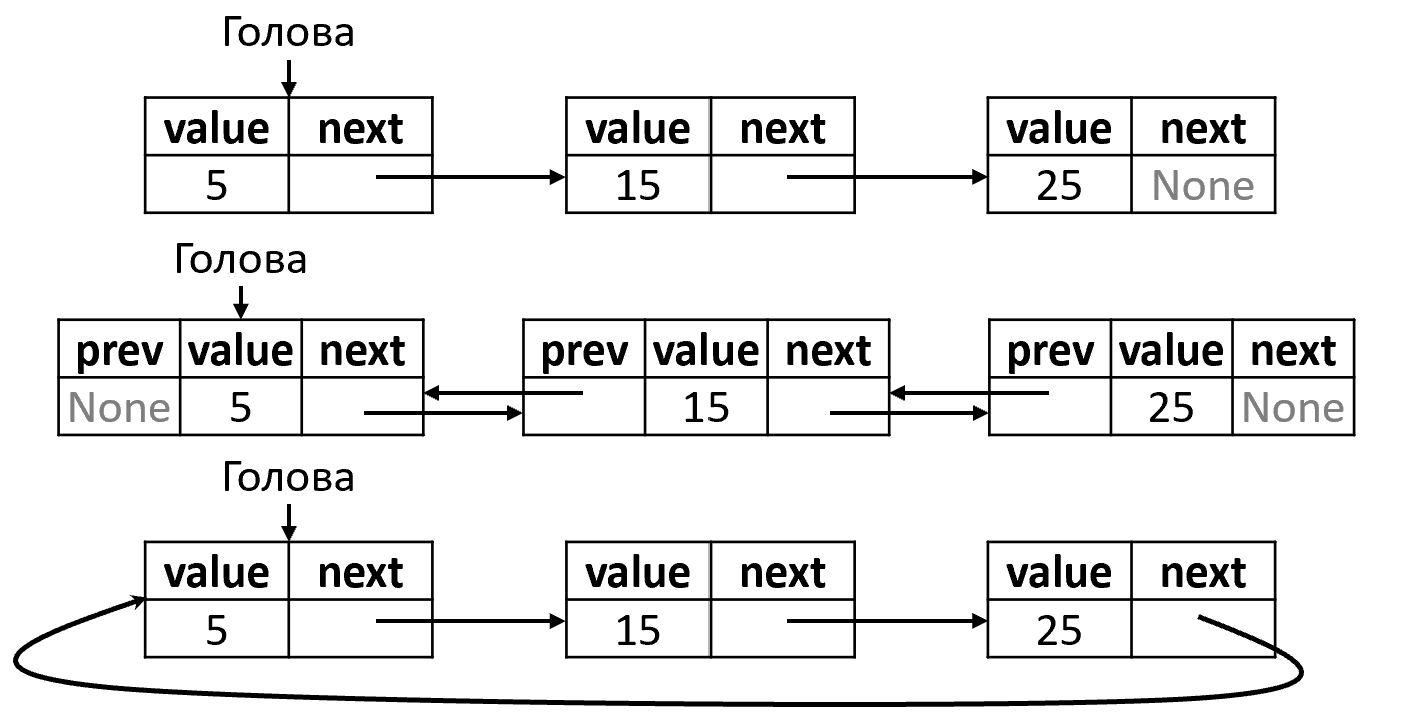
На базе массива или связного списка можно реализовать следующие линейные АТД: список, стек, очередь, дек.
АТД список отражает базовую концепцию линейной последовательности неких элементов. Библиотечные реализации на динамическом массиве обычно носят название ArrayList (Java, C#), Vector (C++) или похожие. Любой список должен реализовывать следующие операции (названия в разных реализациях могут отличаться):
Insert(вставка в произвольную позицию);Delete(удаление из произвольной позиции);Lookup(поиск элемента);PrevиNext(перемещение назад/вперёд по последовательности).
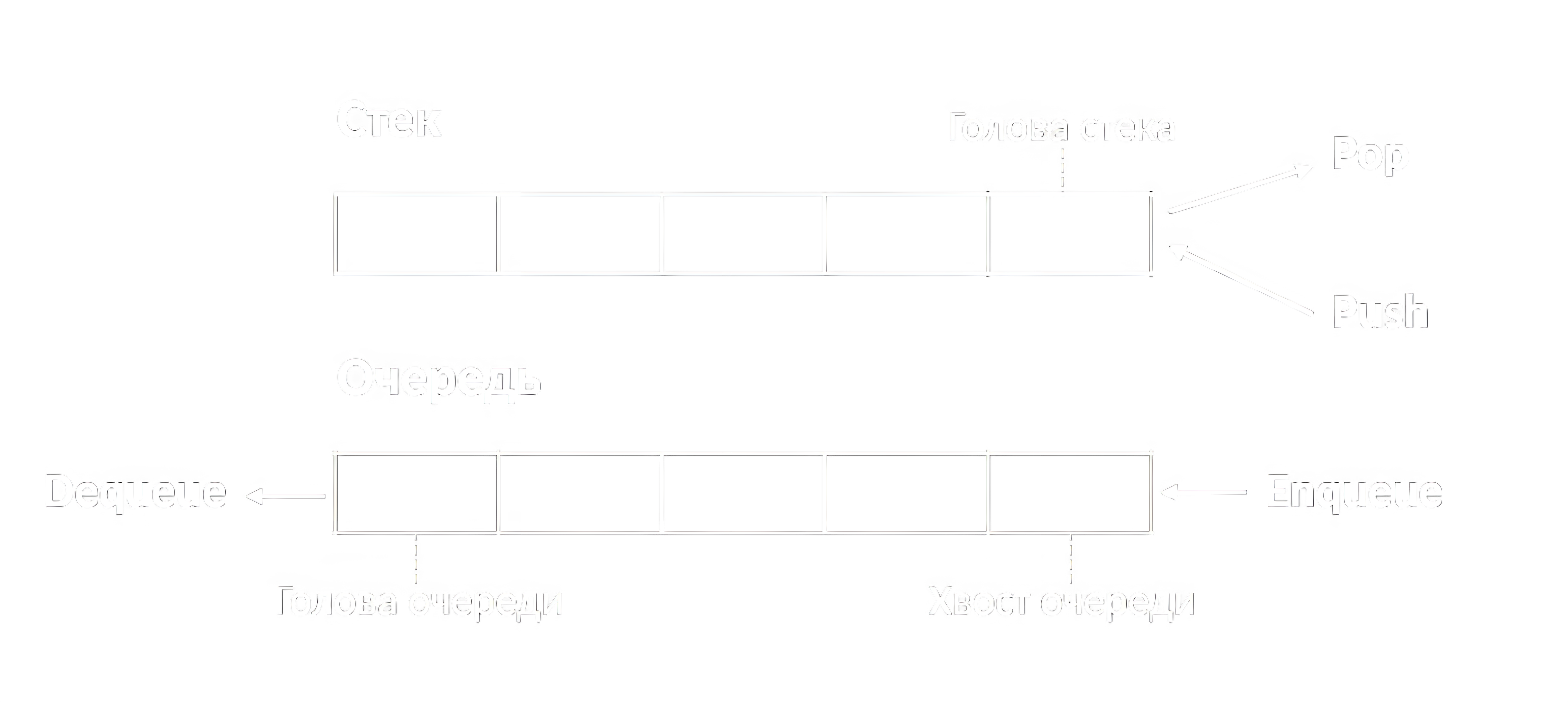
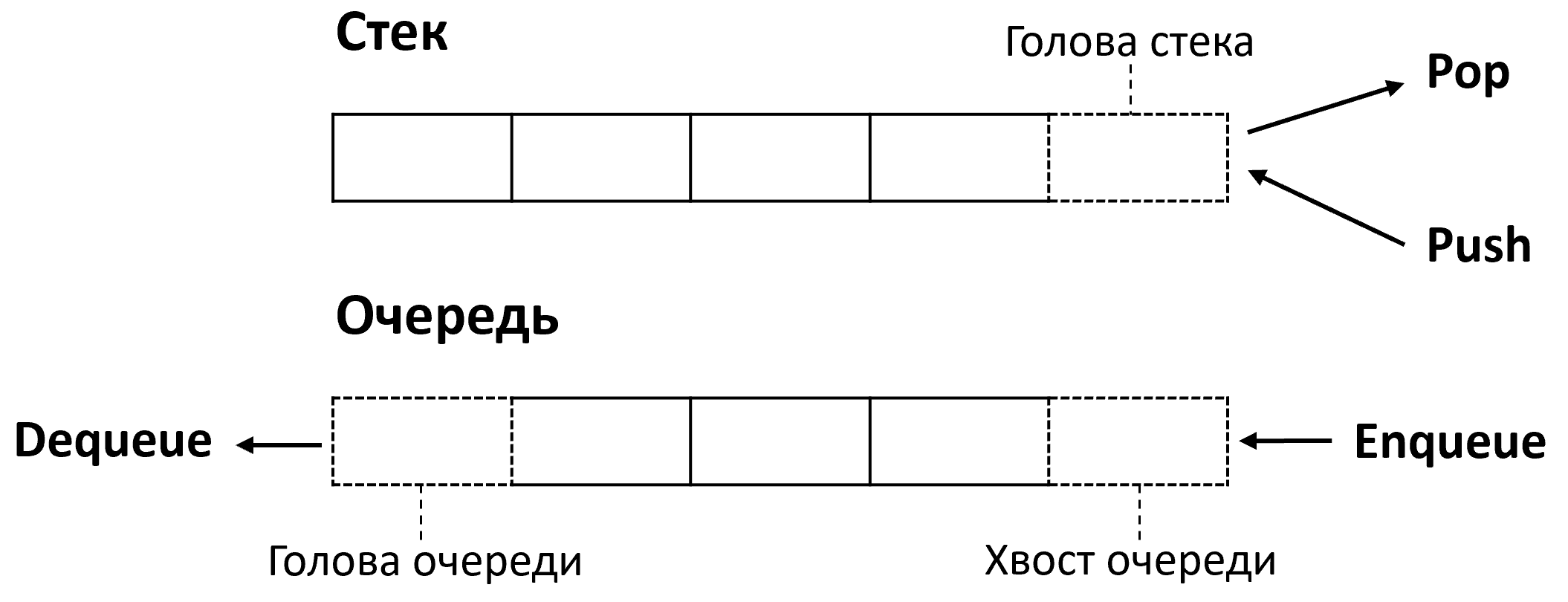
АТД стек (Stack) отражает концепцию стопки элементов, когда что укладка нового (операция Push), что взятие существующего элемента (операция Pop) может производиться только с одного конца (принцип LIFO, «последним пришёл – первым ушёл»). В связи с этим стек эффективно реализуем при помощи массива и целочисленной переменной top (вершины стека), указывающей на следующий свободный индекс. Изначально top = 0. При вставке элемент записывается в ячейку top, затем top увеличивается. При удалении сначала top уменьшается, затем из соответствующей ячейки извлекается значение. Аналогичным образом работает и системный стек, а для размещения указателя на вершину стека используется отдельный регистр процессора.
Стек применяется в различных системах в том числе для хранения истории действий (для отката) или перемещений (как в браузере), разбора выражений в компиляторах, реализации обхода графа в глубину и многого другого. Рекурсивные алгоритмы заастую могут быть переписаны на итеративный вид с использованием собственного стека, чтобы избежать переполнения системного стека.
АТД очередь (Queue) реализует обратный принцип – FIFO («первым пришёл – первым ушёл»). Вставка (Enqueue) производится с одного конца, а изъятие (Dequeue) – с другого (рисунок 3). Очередь можно реализовать как на связном списке, так и на массиве. В последнем случае возможно использование кольцевого буфера – массива с циклическим заполнением и двумя указателями на начало и конец очереди.
Очереди обычно применяются для временного хранения различных поступающих задач, заявок, планирования ресурсов (очереди печати) и подобного. Кроме того, с её помощью реализуется обход графа в ширину.
АТД дек (Dequeue) или двусторонняя очередь – это сочетание стека и обычной очереди. Такая структура позволяет как добавлять, так и забирать элементы с обоих концов линейной последовательности. Может быть реализован на массиве или двусвязном списке.
3.2. Алгоритмы поиска в линейных структурах
В данной и последующих главах идентификаторы элементов, по которым производятся операции поиска, сортировки и другие, будем называть ключами.
Базовый алгоритм поиска в линейных структурах – линейный поиск. Он предельно прост и универсален, т.к. не требует произвольного доступа и применим к связным спискам. Возможность уменьшить сложность с до логарифмической открывается в случае упорядоченных массивов. Здесь уже возможны бинарный и экспоненциальный поиск.
Бинарный поиск (Binary Search) основан на методе «разделяй и властвуй»: диапазон поиска делится пополам, проверяется средний элемент, и в зависимости от результата поиск продолжается либо в левой, либо в правой половине. Алгоритм может быть реализован как рекурсивно, так и итеративно. Итеративная версия приведена в листинге:
def binary_search(array, key):
left = 0; right = len(array) - 1
while left <= right:
mid = (left + right) // 2 # Целочисленное деление
if array[mid] == key:
# Средний элемент оказался искомым
return mid
elif array[mid] < key:
# Сужаем поиск в правой половине
left = mid + 1
else:
# Сужаем поиск в левой половине
right = mid - 1
return -1
Каждый шаг бинарного поиска исключает половину текущего диапазона. Если исходный диапазон имел длину , то после шагов останется . Поиск завершается при достижении длины 1. Следовательно, .
Экспоненциальный поиск (Exponential Search) – модификация бинарного поиска, удобная при работе с потенциально бесконечными последовательностями. Сначала определяется интервал, в котором может находиться ключ: индекс последовательно удваивается, пока не будет найден элемент, не меньший искомого (при упорядоченности по возрастанию). Далее внутри найденного интервала выполняется бинарный поиск. Поиск интервала занимает в худшем случае , бинарный поиск внутри интервала – также , поэтому итоговая сложность остаётся .
def exponential_search(array, key):
if array[0] == key:
return 0
i = 1
while i < len(array) and array[i] < key:
i *= 2
left = i // 2 + 1; right = i # Края интервала
return binary_search(array, left, right, key)
3.3. Алгоритмы сортировки
Сортировка – это упорядочение элементов по неубыванию или невозрастанию ключей. В дальнейшем для простоты будем рассматривать сортировку по неубыванию, а в качестве ключей – сами элементы.
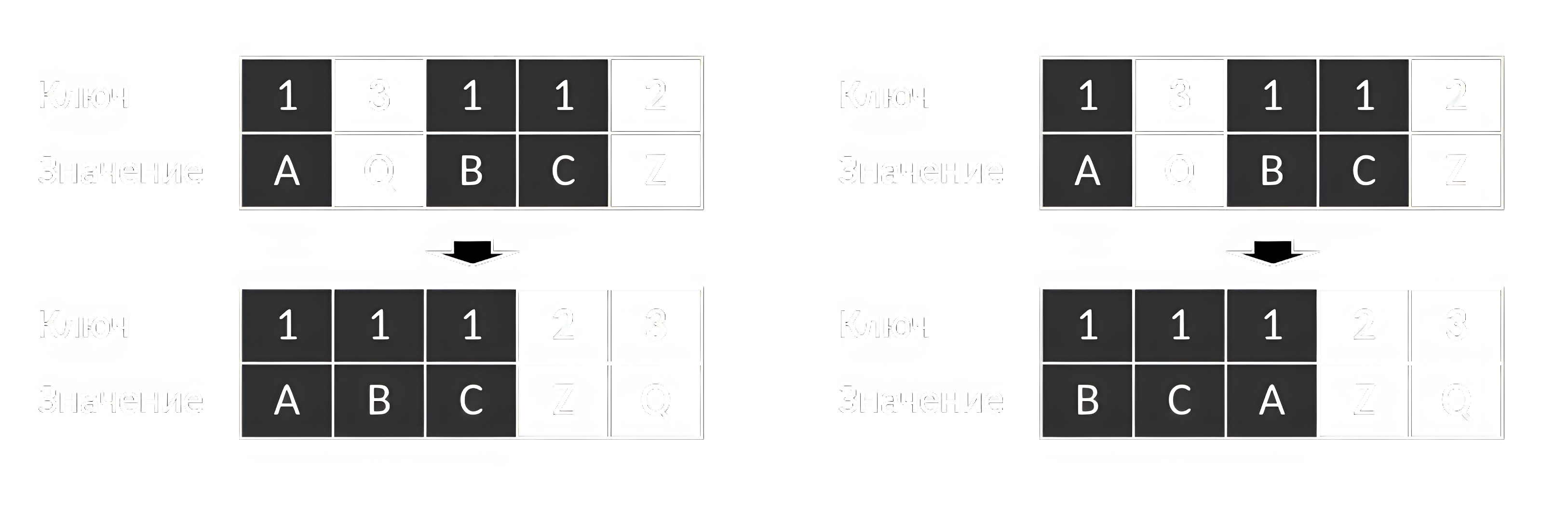
Алгоритмы сортировки различаются не только сложностью, но и такими свойствами, как устойчивость и естественность. Устойчивая сортировка сохраняет относительный порядок равных элементов (рисунок 4). Естественность означает эффективность на частично упорядоченных данных.
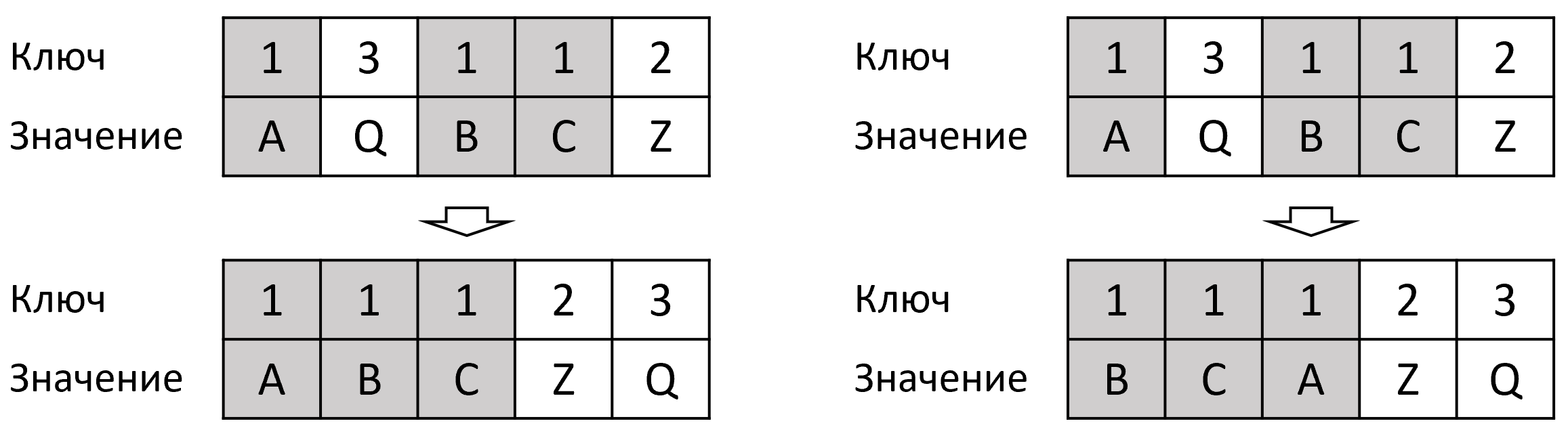
Все алгоритмы общего назначения основаны на сравнениях и имеют фундаментальный предел сложности худшего случая . Однако если диапазон значений ключей ограничен и известен, можно использовать алгоритмы, не основанные на сравнениях, которые работают быстрее.
На практике чаще всего применяются следующие алгоритмы (и их гибриды вроде Timsort): сортировка вставками, быстрая сортировка, сортировка слиянием, поразрядная сортировка. Основные характеристики данных алгоритмов вынесены в таблицу 1.
Таблица 1. Свойства алгоритмов сортировки
| Сортировка | Сложность | Устойчивость | Естественность | Особенности |
|---|---|---|---|---|
| Вставками | Да (в большинстве реализаций) | Да | Возможность упорядочивать динамически поступающие элементы | |
| Быстрая | В среднем: В худшем: | Нет | Нет | Применнимость к связным спискам сомнительна |
| Слиянием | Да | Нет (но есть естественные модификации) | Возможность сортировки данных в долговременной памяти | |
| Поразрядная | По времени: По памяти: – длина ключа (в разрядах) | Да | Нет |
Сортировка вставками (Insertion Sort). Алгоритм постепенно расширяет отсортированную часть последовательности, вставляя новые элементы на нужное место. Псевдокод сортировки приведён в листинге:
def insertion_sort(array):
for i = 1; i < len(array); i++:
key = array[i]
j = i - 1
while j >= 0 and array[j] > key:
# Двигаем элементы вправо, освобождая место для вставки
array[j + 1] = array[j]
j--
array[j + 1] = key # Вставка
return array
Несмотря на квадратичную сложность, сортировка вставками обладает рядом преимуществ: простота, эффективность на небольших последовательностях, естественность, а также возможность упорядочивать динамически поступающие элементы. Приведённый вариант реализации, постепенно проталкивающий очередной элемент на своё место, с минимальными изменениями применим и к связным спискам. Возможно применение бинарного поиска для определения места вставки элемента, но тогда алгоритм потеряет устойчивость и станет не применим к связным спискам.
Быстрая сортировка (Quick Sort). Алгоритм использует метод «разделяй и властвуй»: выбирается опорный элемент, последовательность делится на части меньше/больше опорного, далее сортировка вызывается рекурсивно. Возможны различные стратегии выбора опорного элемента: центральный, первый, последний, случайный и др. Разбиение заключается в перестановке элементов так, чтобы все элементы, меньшие опорного, оказались слева от него, а большие – справа. Возможная реализация алгоритма приведена в листинге:
def quick_sort(array, left, right):
if left >= right:
return
pivot = array[(left + right) // 2]
i = left
j = right
while i <= j:
# Перемещаем i и j к опорному элементу, пока не найдём пару для перестановки
while array[i] < pivot:
i++
while array[j] > pivot:
j--
if i <= j:
# Меняем элементы местами
array[i], array[j] = array[j], array[i]
i++
j--
quick_sort(array, left, j)
quick_sort(array, i, right)
Быстрая сортировка в среднем очень эффективна, естественным образом распараллеливаема и наиболее часто применяется как сортировка общего назначения в стандартных библиотеках. Возможен худший случай, когда выбранный опорный элемент каждый раз оказывается наименьшим или наибольшим, что приводит к квадратичной сложности. Однако такая ситуация крайне маловероятна при адекватной стратегии выбора опорного элемента. Приведённая рекурсивная реализация чувствительна к проблеме переполнения стека, поэтому на практике валидно подменять её на другую, начиная с определённой глубины рекурсии. Применимость для связных списков сопряжена с дополнительными издержками и потому на практике не оптимальна. Кроме того, недостатком является неустойчивость, от которой можно избавиться, но за счёт линейных затрат по памяти и дополнительного прохода.
Сортировка слиянием (Merge Sort). Алгоритм также использует метод «разделяй и властвуй»: последовательность разбивается на две части, которые сортируются рекурсивно, а затем объединяются. Т.е. общую схему алгоритма можно представить так:
def merge_sort(array, left, right):
if left < right:
middle = (left + right) // 2
merge_sort(array, left, middle)
merge_sort(array, middle + 1, right)
merge(array, left, middle, right)
Для сортировки подпоследовательности на любом уровне рекурсии можно переключиться на другую сортировку. Основная сложность алгоритма заключается в объединении отсортированных подпоследовательностей. При сортировке массивов для этого понадобится вспомогательный массив (сложность по памяти), в котором будут накапливаться элементы в отсортированном порядке. При сортировке связных списков дополнительная память не требуется. Приведём псевдокод алгоритма для массивов:
def merge(array, left, middle, right):
i = left
j = middle + 1
k = 0
temp = массив длины (right - left + 1), заполненный нулями
while i <= middle and j <= right:
# Копируем в temp наименьший из двух элементов
if array[i] <= array[j]:
temp[k] = array[i]
i++
else:
temp[k] = array[j]
j++
k++
# Копируем оставшиеся элементы из левой части, если они остались
while i <= middle:
temp[k] = array[i]
i++
k++
# Копируем оставшиеся элементы из правой части, если они остались
while j <= right:
temp[k] = array[j]
j++
k++
# Копируем отсортированные элементы обратно в исходный массив
for k = 0; k < right - left + 1; k++:
array[left + k] = temp[k]
Главная сила сортировки слиянием – это даже не гарантированная логарифмическая сложность (на практике из-за накладных расходов быстрая эффективнее), а её применимость для сортировки данных, находящихся в долговременной памяти. Большинство прочих сортировок требует единовременного нахождения всех данных в оперативной памяти для их обработки. Сортировка слиянием же позволяет обрабатывать данные по частям, что делает её незаменимой в определённых ситуациях. Она также устойчива, не имеет «трудных» входных данных, относительно легко распараллеливается, но неестественна. Кроме того, идеально подходит для сортировки связных списков.
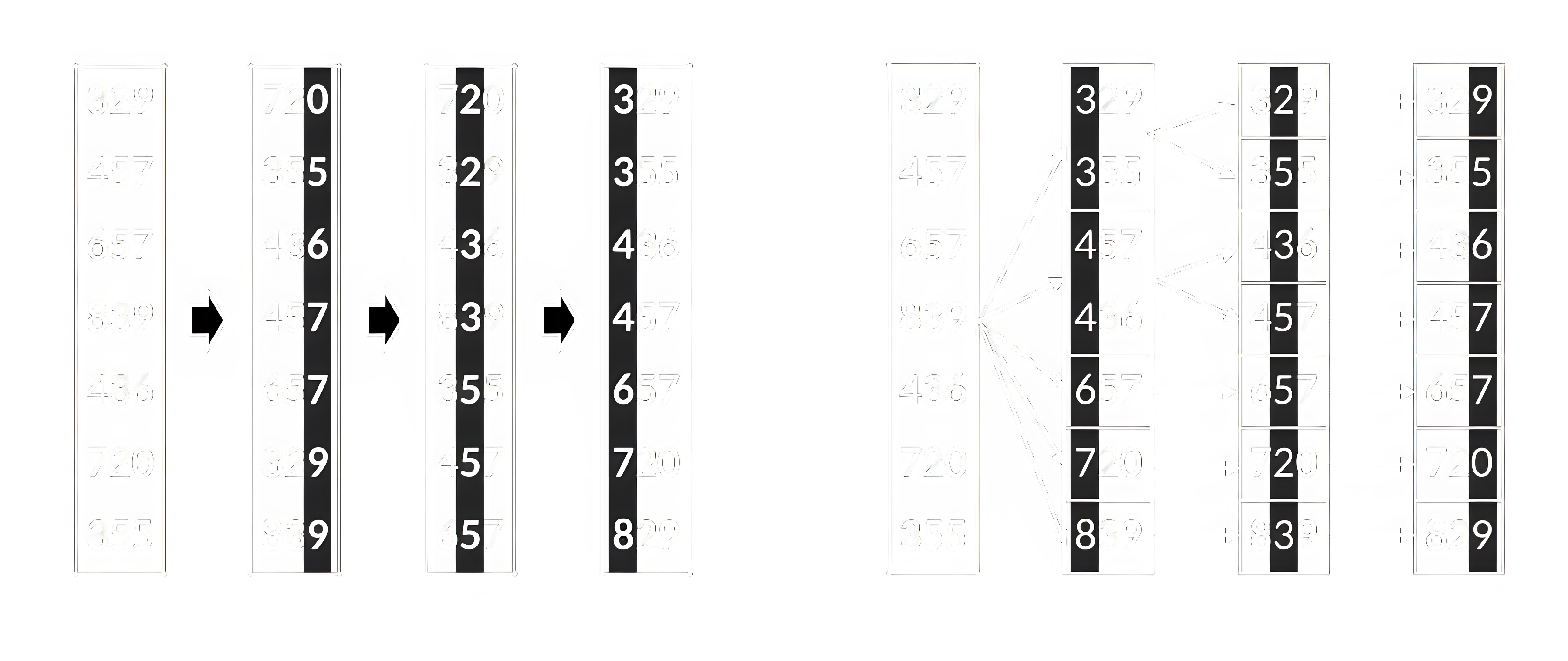
Поразрядная сортировка (Radix Sort). Алгоритм применим к любым типам, для которых валидно понятие «разряд» (числа, строки) и диапазон значений разрядов ограничен. Сортировка выполняется поразрядно: сначала сравнивается один из крайних разрядов, и элементы распределяются на группы в соответствии с его значением (в каждой группе – одинаковые значения разряда, группы упорядочены по значению разряда). Направление обхода разрядов может быть слева направо (Most Significant Digit) или справа налево (Least Significant Digit). При LSD сортировке получается порядок, уместный для чисел, при MSD – алфавитный порядок для строк (символы строки рассматриваем как разряды). После разбиения на группы при MSD сортировке производится рекурсивный вызов сортировки для каждой группы. Итоговая последовательность получается конкатенацией групп в порядке их следования. При LSD сортировке группы не сортируются рекурсивно, а объединяются сразу. Затем рассматривается следующий разряд и, благодаря устойчивости алгоритма, элементы с равенством по более старшему разряду сохранят своё относительное расположение по младшему. Концепция двух вариантов сортировки изображена на рисунке 5.
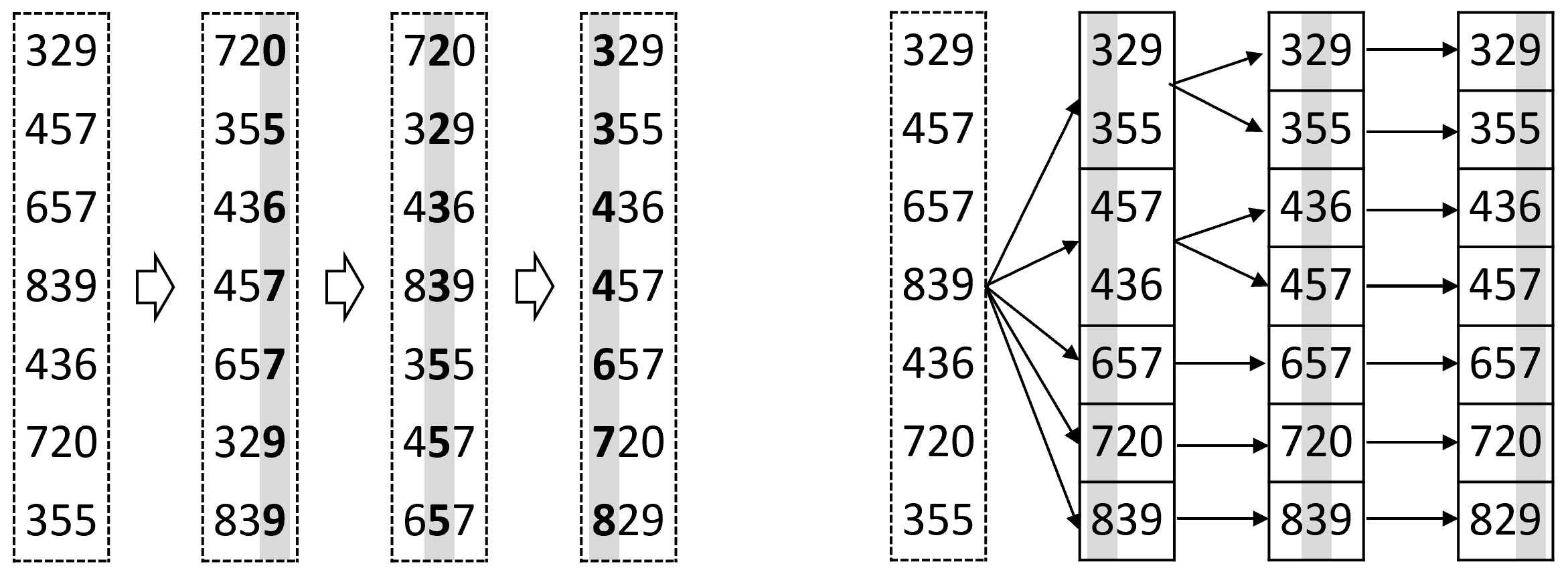
В качестве устойчивого алгоритма сортировки по разряду в LSD обычно используется сортировка подсчётом. Это алгоритм, чья концепция и заключается в заготовке групп (бинов) для всех возможных значений ключа, и последующем переносе элементов в соответствующие группы. В чистом виде сортировка подсчётом фактически не используется, т.к. затраты памяти чувствительны к диапазону значений ключей. Однако диапазон значений разряда всегда сильно ограничен и не зависит от размера входных данных, что и делает поразрядную сортировку эффективной. И поразрядная и сортировка подсчётом обходят предел сортировок общего назначения за счёт того, что не основаны на сравнениях. Это позволяет получить для них линейную оценку сложности.
Помимо описанных 4 алгоритмов для сортировки массивов иногда используется и так называемая пирамидальная сортировка, основанная на бинарной куче. Она эффективна по памяти и обеспечивает гарантию логарифмической сложности. О бинарной куче речь пойдёт в следующей главе.